Récurrence

[Anonyme]

bonjour,
devoir de prépa hec pour la rentée :
à démontrer par récurrence
quelquesoit n appartenant à N
3^(3n+2)+2^(n+4) est divisible par 5
pour n=0 c bon ensuite
on considère que c'est vrai à un certain rang n(superieur à 0)

on doit pouver que 5 | 3^(3n+5)+2^(n+5) ce que je n'arrive pas à faire.
cela doit être tellement simple que j'ai honte mais bon les vacances m'ont complètement rouillé.

merci d'avance.

[dilzydils]

Salut,

Il existe 1 entier k tel que: 3^(3n+2)+2^(n+4)=5k
Ds le coeur du rst par recuurence, tu utilises le fait que:

3^(3n+5)+2^(n+5)=3^3*(3^(3n+2))+2*2^(n+4) (E)
Or 3^(3n+2)=5k-2^(n+4) d'apres l'hypothese de recurrence
Tu remplaces ds ds l'expression (E) puis tu factorises par 5.

:happy2:

[Anonyme]

au rang n+1 t'as donc:
3^3*(3^(3n+2))+2*2^(n+4)
tu factorises par 2, t'as donc
2[(3^(3n+2)+2(n+4)] + 25 [3^(3n+2)]

or (3^(3n+2)+2(n+4) =5k et 25= 5*5 = 5k'
voilà..tu refactorises par 5 et...CDFD!!

[Aldebaran]

Puis je me permettre (en utilisant TEX) de mieux présenter les calculs (afin) que ratata ne se goure pas !
; (A).
Effectivement on factorise par et :
(A) ; (B).
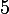or est un multiple de (donc de la forme ) car c'est l'hypothèse de récurrence.
Il ne reste plus qu'à factoriser par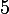 et :
(B)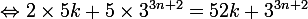
et comme on a bien vérifié la propriété au rang et la récurrence aboutit... :ptdr:

(Je sais je sais, j'ai juste répété ce que vous aviez écrit, mais en fait je m'entraine à écrire en TEX, c'était juste pour le fun quoi !!!) :zen:

[palmade]

Il faut voir que ça marche parce que 3^3=27=25+2 est congru à 2^1=2 modulo 5, donc en passant au rang supérieur on double le terme précédent et on rajoute un multiple de 25, donc de 5 :we: