QQn peutil m'aider car je dois trouver le domaine de définition et l'image d'une fonction. Puis calculer sa réciproque et chercher son domaine de définition et son image. Sachant que le domaine de définition de la fonction va me donner l'image de la réciproque et que le domaine de la réciproque me donnera l'image de la fonction comment dois-je faire ?
Ma fonction est
y= ln (x-2)^-4
y est égal au logarithme naturel de (x-2) exposant -4
merci d'avance...
Réciproque
4 messages
- Page 1 sur 1
Bonjour :happy3:
}) existe sur ]2;3[U]3;+oo[
existe sur ]2;3[U]3;+oo[
Sa dérivée est :
=-\frac{4}{(x-2).ln^{5}(x-2)})
Sur ]2;3[, elle sera positive , sur ]3;+oo[ elle sera négative.
donc f croît sur ]2;3[ et décroît sur ]3;+oo[
Nous avons :


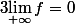
Il est clair que f n'est pas bijective sur ]2;3[U]3;+oo[ donc on ne peut définir de réciproque sur cette réunion d'intervalle.
Par contre , f induit une bijection de ]3;+oo[ sur ]0;+oo[
Ainsi considérons la restriction de f

 est bien une bijection.
est bien une bijection.
}=y\Rightarrow ln^{4}(x-2)=\frac{1}{y}\Rightarrow x-2=e^{\frac{1}{\sqrt[4]{y}}}\Rightarrow x=e^{\frac{1}{\sqrt[4]{y}}}+2)
Ainsi nous obtenons la fonction réciproque recherchée
=e^{\frac{1}{\sqrt[4]{y}}}+2) définie sur ]0;+oo[ et à valeur dans ]3;+oo[
définie sur ]0;+oo[ et à valeur dans ]3;+oo[

Sa dérivée est :
Sur ]2;3[, elle sera positive , sur ]3;+oo[ elle sera négative.
donc f croît sur ]2;3[ et décroît sur ]3;+oo[
Nous avons :
Il est clair que f n'est pas bijective sur ]2;3[U]3;+oo[ donc on ne peut définir de réciproque sur cette réunion d'intervalle.
Par contre , f induit une bijection de ]3;+oo[ sur ]0;+oo[
Ainsi considérons la restriction de f
Ainsi nous obtenons la fonction réciproque recherchée
Hum tu aurais pu mettre des parenthéses ça m'aurait évité de faire tout ça pour rien ...
Je te rappelle notamment qu'avant de parler de réciproque, il faut s'assurer que la fonction est bijective, sinon la réciproque peut être multiforme ...
Pour s'assurer de la bijectivité de la fonction, on peut passer par son sens de variation. Par exemple, la stricte monotonie d'une fonction continue f sur un intervalle I assure la bijectivité de f: I -> f(I)
Essaye de le faire avec la VRAI fonction
:happy3:
Je te rappelle notamment qu'avant de parler de réciproque, il faut s'assurer que la fonction est bijective, sinon la réciproque peut être multiforme ...
Pour s'assurer de la bijectivité de la fonction, on peut passer par son sens de variation. Par exemple, la stricte monotonie d'une fonction continue f sur un intervalle I assure la bijectivité de f: I -> f(I)
Essaye de le faire avec la VRAI fonction
:happy3:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
