Bonjour,
je suis actuellement en licence pro informatique CDED. Dans le cadre d'un de mes projets, je dois réaliser une courbe de tendance polynomiale d'ordre 3.
Je possède un nuage de points... A partir de ces points, il est possible sous Excel de réaliser cette courbe facilement et sans problème.
Le but de mon projet est de ne pas utiliser Excel. Je dois créer un programme permettant à partir du nuage de point de créer cette courbe de tendance. Mais le plus important étant d'avoir l'équation de cette courbe avec ces coefficients...
En espérant avoir des réponses rapidement...
Merci
Réalisation d'une courbe de tendance polynomiale d'ordre 3
7 messages
- Page 1 sur 1
Le plus simple me paraît être le tâtonnement.
Soit ton polynôme : a*X^3 + b*X^2 + c*X + d.
Tu modifies les facteurs de ton polynôme, tu compares les distances entre tes points et ta courbe (tu fais une moyenne), et tu changes les facteurs en fonction de tes résultats précédents.
Tu fais n (n fixé) essais et tu t'arrêtes. Plus n est important, plus ton polynôme est précis.
Une deuxième idée qui me vient à l'esprit : tu regardes les racines de ton polynôme sur la courbe. Tu le factorises et tu le développes, le résultat est-il proche de la courbe ?
Si oui, il peut te servir de base pour le tâtonnement.
Soit ton polynôme : a*X^3 + b*X^2 + c*X + d.
Tu modifies les facteurs de ton polynôme, tu compares les distances entre tes points et ta courbe (tu fais une moyenne), et tu changes les facteurs en fonction de tes résultats précédents.
Tu fais n (n fixé) essais et tu t'arrêtes. Plus n est important, plus ton polynôme est précis.
Une deuxième idée qui me vient à l'esprit : tu regardes les racines de ton polynôme sur la courbe. Tu le factorises et tu le développes, le résultat est-il proche de la courbe ?
Si oui, il peut te servir de base pour le tâtonnement.
J'éviterais.
Comme tu as un nuage de point et que tu recherches une approximation, tu ne sauras pas quels points choisir pour avoir le bon polynôme. Il suffit que tu prennes un seul point un peu trop extrême pour tout fausser.
Mais ça peut servir pour trouver une première forme du polynôme par contre. Le tâtonnement derrière me semble inévitable.
PS : 400 point pour un processeur de 1 Ghz, il doit mettre au moins un quart de second pour le faire, je pense oui. Un quart de quart de second ?
Non, vraiment, c'est rien du tout. A partir de 10.000 points, je commencerais à m'inquiéter avec un ordinateur peu récent et un mauvais programme.
Comme tu as un nuage de point et que tu recherches une approximation, tu ne sauras pas quels points choisir pour avoir le bon polynôme. Il suffit que tu prennes un seul point un peu trop extrême pour tout fausser.
Mais ça peut servir pour trouver une première forme du polynôme par contre. Le tâtonnement derrière me semble inévitable.
PS : 400 point pour un processeur de 1 Ghz, il doit mettre au moins un quart de second pour le faire, je pense oui. Un quart de quart de second ?
Non, vraiment, c'est rien du tout. A partir de 10.000 points, je commencerais à m'inquiéter avec un ordinateur peu récent et un mauvais programme.
Salut,
Perso, j'essayerait avec la bonne vieille méthode des moindres carrés :
Tu dit que tu cherche a,b,c,d tels que la somme des carrés des distance (mesurées verticalement) entre les points du nuage et la courbe d'équation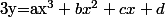 soit minimale.
soit minimale.
Ca te conduit à minimiser la fonction de 4 variables :
=\bigsum_{k=1}^n\left(ax_i^3+bx_i^2+cx_i+d-y_i)^2) (si tes points sont les
(si tes points sont les _{1\leq i\leq n})
qui, si tu développe le carré te donne une gentille fonction de degrés 2 en a,b,c,d.
Tu n'as plus qu'à dire que le minimum est obtenu lorsque les dérivées partielles en a,b,c,d sont nulles et à résoudre ton système (linéaire vu que f est de degrés 2) de 4 équations à 4 inconnues.
Perso, j'essayerait avec la bonne vieille méthode des moindres carrés :
Tu dit que tu cherche a,b,c,d tels que la somme des carrés des distance (mesurées verticalement) entre les points du nuage et la courbe d'équation
Ca te conduit à minimiser la fonction de 4 variables :
qui, si tu développe le carré te donne une gentille fonction de degrés 2 en a,b,c,d.
Tu n'as plus qu'à dire que le minimum est obtenu lorsque les dérivées partielles en a,b,c,d sont nulles et à résoudre ton système (linéaire vu que f est de degrés 2) de 4 équations à 4 inconnues.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Comme j'ai aucune idée de ce qu'est le VBA, c'est pas moi qui pourrait te dire si ça t'aidera.
D'un autre coté, résoudre un système linéaire de 4 équations à 4 inconnues, c'est quand même super facile à mettre en oeuvre sur à peu prés n'importe quel outil informatique...
D'un autre coté, résoudre un système linéaire de 4 équations à 4 inconnues, c'est quand même super facile à mettre en oeuvre sur à peu prés n'importe quel outil informatique...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
