Réalisation séquentielle d'une borne sup/inf

[raito123]

Bonjour,

En lisant un cours a propos des relations d'ordre et les sous-ensemble j'ai trouver ce théorème que je n'ai pas compris :
_______________________________________________________________
Soit A une partie non vide de IR :

1/Il existe tel que

2/ tel que
_______________________________________________________________

c'est quoi le !?

quelqu'un pour m'éxpliquer ce théorème !!?

Merci ++

[mathelot]

wow,

c'est de la langue de bois universitaire :zen: , non, je plaisante.

Les nombres réels sont définis par des coupures (cf Dedekind).
On se donne deux parties A et B telles que:




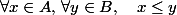
Un couple (A,B) d'enhsembles adjacents définit un nombre.

Exemple, deux suites numériques adjacentes vont définir leur limite commune .

La borne supérieure d'un ensemble A est la coupure
entre A et l'ensemble B de ses majorants.

exemple 1:




l'ensemble B des majorants de f est l'intervalle


on écrit

exemple 2:
le rayon de convergence d'une série entière est la borne supérieure
de l'ensemble des x pour lesquels la série converge.

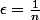
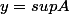
La suite d'éléments de A, suite qui converge vers la borne supérieure: sup A peut être obtenue en prenant et dans la définition.

Ce qu'il faut savoir aussi, c'est que l'ensemble A de rationnels:
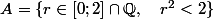
n'admet pas de borne supérieure.

[mathelot]

Maintenant si n'est pas majoré, l'ensemble B de ses majorants est vide, on définit un truc bizarroïde
, qui serait un élément du compactifié
de , le compactifié étant compact et ayant les propriétés d'un intervalle fermé,borné.

Par exemple, est obtenu à partir de en rajoutant deux points aux extrémités, de manière que
la fonction soit continue de codomaine

peut être vu comme un arc de cercle,
simplement connexe.

Par contre, avec le compactifié d'Alexandroff de ,
on ne rajoute qu'un seul point à l'infini, ce qui le rend compact, homéomorphe
à un cercle , non simplement connexe, mais détruit la relation d'ordre.

[ThSQ]

Lol, je crois qu'il veut juste savoir ce que c'est que non ?

C'est R à qui on a adjoint deux symboles +°° et -°° respectivement + grand et + petit que tout les autres.

Ca s'appelle aussi la droite numérique achevée

Et le théorème c'est : on peut trouver une suite qui converge vers borne sup qu'elle soit finie ou non

[raito123]

O_o !!!

Merci pour ta réponse mathelot !

y a bcp de notions pas encore vu ( ben oui je viens d'avoir mon bac la semaine derniére mdr^^)!!

une coupure c'est l'interséction !?

le rayon de convergence d'une série !?

élément commpactifié?

codomaine?

Merci++

[raito123]

Lol, je crois qu'il veut juste savoir ce que c'est que non ?

C'est R à qui on a adjoint deux symboles +°° et -°° respectivement + grand et + petit que tout les autres.

Ca s'appelle aussi la droite numérique achevée

Et le théorème c'est : on peut trouver une suite qui converge vers le plus grand élément, qu'il soit fini ou non

Ok merci^^!

[raito123]

Ok merci ThSQ !!

[mathelot]

y a bcp de notions pas encore vu ( ben oui je viens d'avoir mon bac la semaine derniére mdr^^)!!

ah, pardon. j'espère que tu vas en sup !! Tu vas voir tout ça au fur et à mesure, tu vas te régaler.

Dans la définition de coupure, on se fiche de savoir si elle appartient à A ou à B.

c'est pour cela que sup A est parfois le plus grand élément de A ,si elle
appartient à A, parfois seulement un majorant, (et alors le plus petit des majorants) si sup A n'appartient pas à A.

[raito123]

Oui je vise les prépas !!

Merci !++