Rationnel et Réel

par **hazaki** » 05 Oct 2010, 20:35

Bonjour,

J'ai un exo à faire pour le prochain TD que je n'arrive pas à attaquer.

Soient x,y appartenant a Q+ tels que sqrt(x) ou sqrt(y) soient irrationnels. Montrer que sqrt(x) + sqrt(y) est irrationnel.

Par quel méthode puis-je commencer ma démonstration? Une méthode par l'absurde serait-elle envisageable?

Merci d'avance pour toute piste de réflexion.

par **Ben314** » 05 Oct 2010, 20:54

Salut,
Plutôt que l'absurde, je ferais une contraposée (on voit nettement mieux ce qu'on fait) en supposant uniquement que la somme des racines est rationelle.
Tu en déduit facilement que le produit des deux racines est rationelle.
Ensuite, tu en déduit que la somme des deux multiplié par le produit des deux est rationnel puis... tu termine (deux cas à traiter selon que x=y ou non)

par **hazaki** » 05 Oct 2010, 21:14

Merci de ta réponse, je suis donc arrivé à sqrt(xy) est rationnel. Mais je vois pas comment on passe à la somme des deux multiplié par le produit des deux.

par **hazaki** » 05 Oct 2010, 21:57

Donc j'en déduis que x * sqrt(y) + y * sqrt (x) est rationnel ?

par **Doraki** » 05 Oct 2010, 22:01

Je sais pas trop comment il voulait poursuivre ou s'il a mal tapé un truc.

Tu peux montrer que (sqrt(x)+sqrt(y))(sqrt(x)-sqrt(y)) est rationnel ?

Que se passe-t-il si sqrt(x)-sqrt(y) est rationnel ?

par **Ben314** » 05 Oct 2010, 22:03

On suppose que

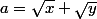
est rationnel (avec x,y rationnels).

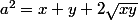
l'est aussi donc il en est de même de

.
Le produit

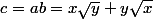
est donc lui aussi rationnel et tout cela commence fort à ressembler à un système de deux équations à deux inconnues...

par **hazaki** » 05 Oct 2010, 22:15

Ben314 : j'etais arrivé à x * sqrt(y) + y * sqrt (x) rationnel mais je vois pas du tout ton système.

Doraki : Dans ce cas sqrt(x) + sqrt(y) est rationnel. Mais je vois pas pourquoi essayes de démontrer que (sqrt(x)+sqrt(y))(sqrt(x)-sqrt(y)) est rationnel.

par **Ben314** » 05 Oct 2010, 22:27

Pour "ma" soluce, le système c'est :

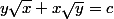
où x,y,a,c sont des rattionnels

Si tu prend la "soluce Doraki" qui est plus simple, tu tombe aussi sur un système qui est :

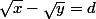
où a,d sont des rationnels

par **hazaki** » 05 Oct 2010, 22:42

Ah ok, mais comment on prouve (pour la soluce de doraki) que sqrt(x) - sqrt(y) est rationnel ?

par **Ben314** » 05 Oct 2010, 22:47

Par hypothèse,

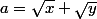
est rationnel.
Mais

est aussi rationnel vu que x et y le sont.
donc...

par **hazaki** » 05 Oct 2010, 22:57

Ah oui en effet merci ^^.
Par contre j'essaye de résoudre le système mais je vois pas trop par quel bout le prendre en fait.

par **hazaki** » 05 Oct 2010, 23:05

Ah je crois que j'ai compris,
je mets a = p/q et d = r/s
donc dans le systeme, je soustrais L1 avec L2 donc j'ai
2 sqrt(x) = (p1q2+p2q1)/q1q2. Ainsi sqrt(x) est rationnel.

par **Ben314** » 05 Oct 2010, 23:07

Avec la "méthode Doraki", ça saute aux yeux !!!
Si tu ajoute les deux tu en déduit que... et si tu soustrait les deux tu en déduit que...

Avec "ma" méthode, il faut faire y fois la première moins la seconde ou bien x fois la première moins la seconde.

par **hazaki** » 05 Oct 2010, 23:37

je mets a = p1/q1 et d = p2/q2
donc dans le systeme, je soustrais L1 avec L2 donc j'ai
2 sqrt(x) = (p1q2+p2q1)/q1q2. Ainsi sqrt(x) est rationnel.

Rationnel et Réel

Rationnel et Réel

Qui est en ligne