Zeitblom a écrit:Bonjour,
(
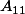
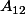
)
(
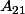
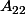
)
est une matrice nxn définie par blocs, de rang r.
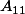
est de taille rxr et de rang r.
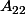
est de taille (n-r)x(n-r). Il s'agit de montrer que
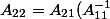A_{12})
. Quelqu'un aurait-il une idée ?
Si la matrice A est de rang r, et que la matrice

est elle aussi de rang r, cela implique que la matrice

est elle aussi de rang r, d'une part, que chacune des colonnes numéros r+1 à n de la matrice A est combinaison linéaire des r premières colonnes.
Il existe donc r coefficients

tels que :

De même, il existe r coefficients

tels que :

Ceci est vrai pour toutes les colonnes de numéros r+1 à r+(n-r) :
Il existe r coefficients

tels que :

Soit :

Les n-r égalités ci-dessus peuvent s'écrire en une égalité matricielle :

Les matrices

et

étant formées respectivement des colonnes 1 à r de A et des colonnes (r+1) à n de A.
Et de manière plus détaillée par blocs :


Comme

est de rang r donc inversible on peut multiplier à gauche les deux membres de la première égalité par
^{-1})
^{-1}A_{12} = \Large (A_{11})^{-1}A_{11}\Lambda= \Lambda)
Et finalement, en remplaçant

par son expression, dans la deuxième égalité matricielle :
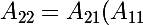^{-1}A_{12})
qui est la relation demandée.
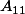
)
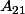
)
est de taille rxr et de rang r.
est de taille (n-r)x(n-r). Il s'agit de montrer que
. Quelqu'un aurait-il une idée ?