Question sur la résolution d'équations...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
par balteo » 03 Déc 2009, 08:30
Bonjour,
J'ai deux équations presque identiques:
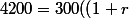^{-1}+(1+r)^{-2}+(1+r)^{-3}+(1+r)^{-4}+(1+r)^{-5}+(1+r)^{-6})+4000(1+r)^{-7})
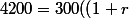^{-1}+(1+r)^{-2}+(1+r)^{-3}+(1+r)^{-4}+(1+r)^{-5}+(1+r)^{-6})+4500(1+r)^{-7})
Remarquez la différence vers la fin: 4000 et 4500.
Je me demande juste d'un point de vue mathématique pourquoi la deuxième équation est plus facilement résolue que le première qui elle a plusieurs racines dont certaines complexes?
Merci,
Julien.
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
par gdlrdc » 03 Déc 2009, 13:46
En posant X= (1+r)^(-1).
On obtient deux équations de degré 7.
La première équation ayant plusieurs racines, on peut baisser son degré par factorisation et donc sa complexité.
ça te parait clair?
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
par gdlrdc » 03 Déc 2009, 13:54
1ère equation:
4200= f(x), on pose g(x)= f(x) -4200
g s'annule une seule fois sur R, donc un raisonnement simple par dichotomie permet de trouver la racine.
Alors que dans le 2ème cas, le nombre de racine complique la recherche.
C'est assez clair?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
