Question suite (facile)

[karimsqualli96]

bonjours voici une suite : Un = (n)/(n+1) j'ai montré quelle est croissante, puis je dois montrer quelle est borné, j'ai dit que puisqua la suite est croissante elle est minoré par u0=0 mais je bloque quand je veux determiner l'autre borne

[capitaine nuggets]

Salut !

bonjours voici une suite : Un = (n)/(n+1) j'ai montré quelle est croissante, puis je dois montrer quelle est borné, j'ai dit que puisqua la suite est croissante elle est minoré par u0=0 mais je bloque quand je veux determiner l'autre borne

Sachant que est strictement croissante, tu as :+++:

[Ezra]

bonjour, voici une suite : Un = (n)/(n+1) j'ai montré quelle est croissante, puis je dois montrer quelle est bornée, j'ai dit que puisque la suite est croissante, elle est minorée par u0=0 mais je bloque quand je veux déterminer l'autre borne

, calcule : puis :

[Robic]

capitaine nuggets : ce serait vrai si la suite admettait une limite, ce qu'on ne sait pas (et c'est sans doute pour le démontrer qu'on vérifie qu'elle est croissante et majorée).

Ezra : tu es sûr que ça prouve quelque chose ? Si je définis la suite , alors j'ai qui tend vers 1 (*), et pourtant la suite n'est pas bornée.

(*) Car :
.

En fait, le but va probablement être de dire que la suite est croissante et majorée, donc admet une limite. Pour montrer qu'elle est majorée, c'est enfantin, ça se voit comme le nez au milieu du visage. Non ? Je recopie la définition : .

Il y a besoin de réfléchir pour voir que c'est plus petit que 1 ? :marteau:

----
Un contre-exemple plus simple que celui avec le logarithme : .
Alors tend vers 1 et pourtant la suite n'est pas bornée.

[Ezra]

Ezra : tu es sûr que ça prouve quelque chose ? Si je définis la suite , alors j'ai qui tend vers 1 (*), et pourtant la suite n'est pas bornée.

(*) Car :
.

En montrant que : on prouve que : est croissante. si : , existe.

[Robic]

(Ah, tu as corrigé.) J'avoue que je ne comprends pas la dernière propriété ni en quoi elle permet de prouver que la suite est majorée. Ah, de toute façon on a pour tout n (j'ai vérifié, les calculs sont fastidieux mais je les ai refaits...)

[Ezra]

Dans ton premier message, tu disais qu'il fallait calculer la limite des Rn : ça ne prouve rien.

À présent tu dis qu'il faut utiliser : . et (puisque la suite des Un est croissante).
..

Une suite croissante et majorée admet une limite et on peut montrer la croissance et la majoration ainsi.
Une suite décroissante et minorée admet une limite et on peut démontrer la décroissance et minoration.

[Robic]

Une suite croissante et majorée admet une limite et on peut montrer la croissance et la majoration ainsi.

Je ne suis pas sûr, mais tu as l'air de dire (pas très clairement) que pour montrer que la suite est majorée, on peut montrer qu'elle est croissante et admet une limite, c'est bien ça ? Oui, mais il faut prouver qu'elle admet une limite (ce qui n'est pas difficile, certes).

Mais bon, le plus simple reste de démontrer que la suite est majorée directement, ça prend dix secondes.

[deltab]

Bonsoir.

>> Karim
Je ne vois pas la relation entre le titre du post et ce tu as fait. Le calcul de ne nécessite pas qu'on montre que (u_n) est croissante bornée sauf si bien sur c'était précisément la question.

>> Capitaine.
Montrer que si (u_n) est strictement croissante bornée, alors peut donner éventuellement la monotonie (u_n). Tu anticipes ici sur la règle de D'Alembert pour les séries à termes positifs qui ne permet, dans le cas ni de déterminer la nature de la série 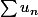ni celle de la suite .