Question à propos de double limite

[MoonX]

Bonjour,

J'ai du mal à comprendre quelque chose, lorsque j'ai une série de fonction , convergente sur son domaine ouvert de convergence, et que je considère la limite aux bornes de ce domaine.

Pour expliquer mon incompréhension, je vais donner un exemple :

J'ai suite de fonction qui, lorsque pour tout s>1.
Il est bien connu que la fonction zeta admet une limite infinie en 1+. Et c'est donc là que j'ai du mal à comprendre.
Est-ce qu'on a le droit de dire que, lorsque la série ? Est-il possible de montrer dans ce cas précis que ?

[Ben314]

Salut,
C'est pas clair ton truc :

J'ai suite de fonction qui, lorsque pour tout s>1.

Ton équivalent, c'est effectivement pour (tout) s>1 fixé et n qui tend vers l'infini ? (si c'est bien ça, ce qui me perturbe, c'est que tu écrive pas)
Et le qui apparait dans l'équivalent, c'est quoi sa "nature" ? (i.e. il dépend du fixé ou pas ?)

Bon, sinon, de toute manière, lorsque tu as à évaluer , ben ça signifie (par définition) que tu as à évaluer et tu ne risque pas de permuter "gratuitement" (i.e. sans hypothèses relativement fortes) les deux limites.

[MoonX]

Merci pour votre réponse.

Oui pardon, j'ai pas été clair vous avez raison, il s'agit bien de . Et A est un réel fixé indépendant du s.

Pour permuter les deux limites, il faut en général monter la convergence uniforme. Supposons alors que je puisse montrer que converge uniformément sur tout segment de pour continuer avec mon exemple.

C'est lorsque qu'on est dans le cas limite que j'ai du mal à comprendre : lorsque l'on s'intéresse à la limite en , est-ce que j'ai la possibilité d'obtenir un équivalent ou même un développement comme j'ai proposé dans mon message initial ?

[Ben314]

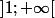
Supposons alors que je puisse montrer que converge uniformément sur tout segment de pour continuer avec mon exemple.

Ben non : si tu as uniquement la C.V.U sur tout segment contenu dans ]1,+oo[, tu peut rien permuter du tout et ça te donne aucune info. sur ce qui se passe en 1^+.
Pour pouvoir permuter, il te faudrait bien sûr la C.V.U. sur un intervalle du style ]1,1+epsilon].
Ca peut aussi fonctionner avec d'autre propriétés (monotonie, croissance, etc...) mais bien sûr, il faut que ce soit valable sur un intervalle du type ]1,1+epsilon] et pas uniquement sur les segments contenus dans ]1,+oo[.

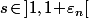
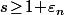
Pour te donner "LE" exemple qui montre le problème, c'est si tes fonctions elles sont définies par pour puis pour (avec ).
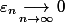
Pour [a,b] contenu dans ]1,+oo[ fixé et suffisamment grand on aura sur [a,b], mais en ce qui concerne la limite de quand s->1+, il est plus que probable que ça dépende de la vitesse à laquelle les tendent vers 0 ce que tu ne peut pas repérer en regardant uniquement ce qui se passe sur des intervalles [a,b] contenu dans ]1,+oo[.