A++
Quel est le type d'un n-uplet qui contient un n-uplet ?
6 messages
- Page 1 sur 1
Quel est le type d'un n-uplet qui contient un n-uplet ?
Bonjour à tous. Je me demandais comment on exprimait le type d'un n-uplet qui contenait un n-uplet. Par exemple le type d'un couple d'entiers naturels est 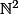 ou
ou 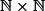 . Mais comment exprime-t-on le type d'un couple dont le premier élément est un entier naturel et le second élément un couple d'entier naturel ? Je sais bien qu'un tel type est équivalent au type qu'on exprime par
. Mais comment exprime-t-on le type d'un couple dont le premier élément est un entier naturel et le second élément un couple d'entier naturel ? Je sais bien qu'un tel type est équivalent au type qu'on exprime par 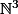 ou
ou  , mais pour des raisons esthétiques je voudrais exprimer le type du couple que je décris, comment faire s'il-vous-plait ? Je précise que je ne suis pas du tout mathématicien, d'où cette question qui peut vous paraître incongrue.
, mais pour des raisons esthétiques je voudrais exprimer le type du couple que je décris, comment faire s'il-vous-plait ? Je précise que je ne suis pas du tout mathématicien, d'où cette question qui peut vous paraître incongrue.
A++
A++
Bonjour.
L'ensemble le plus approprié est .
.
Tout élément de cet ensemble est un couple, le premier élément est dans , le second dans
, le second dans 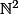 , c'est à dire lui même un couple d'entiers. Au final, un tel élément se note
, c'est à dire lui même un couple d'entiers. Au final, un tel élément se note )) . (en général, on supprime les parenthèses inutiles, et on considère cet ensemble comme étant
. (en général, on supprime les parenthèses inutiles, et on considère cet ensemble comme étant 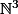 )
)
L'ensemble le plus approprié est
Tout élément de cet ensemble est un couple, le premier élément est dans
Bonjour,
Il y a un isomorphisme canonique entre ces deux ensembles (i.e. un moyen évident de faire correspondre un élément de à un élément de
à un élément de 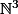 et réciproquement), si bien qu'on considère effectivement que c'est « la même chose » sans même dire qu'on fait cette identification. Après il peut y avoir des moments où veut quand même faire la distinction.
et réciproquement), si bien qu'on considère effectivement que c'est « la même chose » sans même dire qu'on fait cette identification. Après il peut y avoir des moments où veut quand même faire la distinction.
Philippe.Lemoine a écrit:Merci beaucoup, j'y avais pensé, mais je croyais queétait strictement la même chose que
, autrement dit qu'un élément de
avait la forme (x, y, z) et non (x, (y, z)).
Il y a un isomorphisme canonique entre ces deux ensembles (i.e. un moyen évident de faire correspondre un élément de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
