Bonjour,
A-t'on le droit de "simplifier" \sqrt{u^2} = (u^2)^(1/2) = u ?
C'est pourtant ce que font gaillardement les étudiants (et pas qu'eux) !
si j'ai (u^n)^(1/n) il semble que u doit être positif. Si je prends le cas de n =3, la fonction cube est une bijection sur R, donc si u = -27, je peux extraire la racine cubique par la fonction réciproque, à savoir -3.
En python (-27)**(1./3) donne lieu à un beau message d'erreur. Sur une HP42S, le résultat est complexe et sous Excel la formule ne le gêne pas. Excel accepte ce genre de formule sans sourciller.
plus généralement peut-on écrire (a^n)^p = (a^p)^n = a^(np) dans tous les cas ?
Merci de vos lumières
Micercle
Puissances nièmes
6 messages
- Page 1 sur 1
Re: puissances nièmes
Salut,
Non on n'a pas toujours le droit de le faire.
Surtout quand il s'agit de nombres négatifs et des exposants comme 1/2
Exemple (-1)^2 existe mais [(-1)^(1/2)]^4 n'est pas défini.
Mais aussi on ne peut pas définir systématiquement une unique puissance 1/3. Par exemple que vaut (-8)^(1/3) ? il y a trois nombres complexes dont un réel tels que leur cube vaut -8. Si on veut on peut choisir de prendre le réel (-2) pour des raisons pratiques ou par définition. Mais des fois on a besoin des trois racines 3ièmes de -8.
C'est pareil avec la racine carrée: si on cherche z tel que z^2=a on peut toujours trouver deux complexes qui marchent. Des fois, ces deux complexes sont en fait deux réels (quand a est positif) donc on choisit celui parmi lesquels est positif. Ce n'est qu'un choix/une définition. Mais on pourrait des fois avoir besoin des deux ..
Pour te renseigner plus cherche 'racine n-ième de l'unité'.
Donc je ne donnerais pas tort à l'un ou à l'autre des logiciels: il se peut qu'ils te donnent une des racines troisièmes de leurs choix.
Non on n'a pas toujours le droit de le faire.
Surtout quand il s'agit de nombres négatifs et des exposants comme 1/2
Exemple (-1)^2 existe mais [(-1)^(1/2)]^4 n'est pas défini.
Mais aussi on ne peut pas définir systématiquement une unique puissance 1/3. Par exemple que vaut (-8)^(1/3) ? il y a trois nombres complexes dont un réel tels que leur cube vaut -8. Si on veut on peut choisir de prendre le réel (-2) pour des raisons pratiques ou par définition. Mais des fois on a besoin des trois racines 3ièmes de -8.
C'est pareil avec la racine carrée: si on cherche z tel que z^2=a on peut toujours trouver deux complexes qui marchent. Des fois, ces deux complexes sont en fait deux réels (quand a est positif) donc on choisit celui parmi lesquels est positif. Ce n'est qu'un choix/une définition. Mais on pourrait des fois avoir besoin des deux ..
Pour te renseigner plus cherche 'racine n-ième de l'unité'.
Donc je ne donnerais pas tort à l'un ou à l'autre des logiciels: il se peut qu'ils te donnent une des racines troisièmes de leurs choix.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: puissances nièmes
Je conviens des racines nièmes dans C, mais -8 est aussi le cube de -2 dans R
La raison pour laquelle x^(1/n) nécessite que x soit>0 est que x^a est défini par exp(a ln(x)) d'ou le x > 0
J'ai bien appris tout ça mais le coup de la réciproque de x^3 me chagrine
Micercle
La raison pour laquelle x^(1/n) nécessite que x soit>0 est que x^a est défini par exp(a ln(x)) d'ou le x > 0
J'ai bien appris tout ça mais le coup de la réciproque de x^3 me chagrine
Micercle
Re: puissances nièmes
En fait le choix de ces logiciels peut-être lié au choix de la branche principale de la fonction multiforme z>z^(1/3).
On peut choisir de définir la fonction racine cubique sur R- en associant à chaque réel négatif l'unique nombre réel négatif qui au cube donne le nombre initial.
Mais rien n'empêche de choisir autre chose qu'un réel pour quelques raisons(pourquoi?).
On peut choisir de définir la fonction racine cubique sur R- en associant à chaque réel négatif l'unique nombre réel négatif qui au cube donne le nombre initial.
Mais rien n'empêche de choisir autre chose qu'un réel pour quelques raisons(pourquoi?).
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: puissances nièmes
Salut,
Personnellement, pour "lever l'ambiguïté", :
- Ce que je note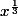 c'est
c'est )) donc défini uniquement pour x>0 (et éventuellement x=0 en prolongeant par continuité) avec comme unique exception (bien sûr...) les puissances entières où x peut être négatif.
donc défini uniquement pour x>0 (et éventuellement x=0 en prolongeant par continuité) avec comme unique exception (bien sûr...) les puissances entières où x peut être négatif.
- Par contre, la bijection réciproque de la fonction de R->R ; x->x^3 (sur R tout entier, mais évidement pas sur C), je la note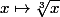 .
.
Par exemple,^{\frac{1}{3}) n'existe pas, mais
n'existe pas, mais 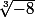 existe et vaut -2.
existe et vaut -2.
Par contre, je sais pas si c'est archi conventionnel comme... convention...
Personnellement, pour "lever l'ambiguïté", :
- Ce que je note
- Par contre, la bijection réciproque de la fonction de R->R ; x->x^3 (sur R tout entier, mais évidement pas sur C), je la note
Par exemple,
Par contre, je sais pas si c'est archi conventionnel comme... convention...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: puissances nièmes
Mais au moins c'est plus clair !
Moralité, faut se méfier des outils de calculs !!! Mais les jeunes bacheliers n'y ont pas été sensibilisés, me semble-t-il !!
Merci d'avoir rallumé la lumière de ma lanterne.
Micercle
Moralité, faut se méfier des outils de calculs !!! Mais les jeunes bacheliers n'y ont pas été sensibilisés, me semble-t-il !!
Merci d'avoir rallumé la lumière de ma lanterne.
Micercle
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
