Prouver la surjectivité d'une fonction

[Stanley]

Bonsoir à tous !
Voila j'ai un problème, je butte sur le corrigé d'un exercice. Je soupçone une erreur dans le corrigé (c'est tiré d'un livre). Quelqu'un pourrait-il me confirmer qu'il y a erreur ou m'expliquer ce qui m'échappe s'il vous plait ?

Enoncé :
Soient E un ensemble non vide et A et B deux parties de E. On considère l'application de P(E) dans (P(E))^2 définie par f(X)=(AuX,BuX) (u désigne l'union)
f peut-elle être surjective ?

Corrigé :
Si f est surjective, alors il existe X tel que f(X)=(;),;)), ce qui nécessite A=B=;). Mais alors, pour tout X, f(X)=(X,X) et f(P(E)) ne peut pas être égal à (P(E))^2. Donc f ne peut pas être surjective

Je comprend pas la phrase en gras. Pour moi, si A=B=;), elle est surjective, puisque pour nimportequel couple (X,X) pris dans (P(E))^2, il existe un X appartenant a P(E) tel que f(X)=(X,X)

Par avance, merci pour votre aide et bonne soirée

[tize]

Bonjour,
ba oui f ne peut pas être surjective car pour toute partie X de E on aurait f(X)=(X,X), il est donc impossible d'obtenir avec .

[Stanley]

Merci pour la réponse. Je suis désolé, je ne comprend toujours pas.

Pourquoi C ne doit pas être égal à D ?

[Skullkid]

Bonsoir, comme dit précédemment, dans le cas où 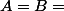, pour tout X, f(X)=(X,X). Mais tout élément de P(E)² ne peut pas s'écrire sous la forme (X,X) : un élément de P(E)² est un couple (X,Y) dans lequel Y n'a aucune raison d'être égal à X.

Plus concrètement : si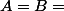 , alors n'a pas d'antécédent par f (puisque E est non vide).

[Stanley]

Mais tout élément de P(E)² ne peut pas s'écrire sous la forme (X,X) : un élément de P(E)² est un couple (X,Y) dans lequel Y n'a aucune raison d'être égal à X.

J'ignorai totalement cela. Pour moi la définition d'un élément de P(E)xP(E) c'est un couple (X,Y) avec X apartenant à P(E) et Y appartenant a P(E), et je pensai que les deux pouvaient être égaux...

Merci pour vos réponses

[Skullkid]

La définition que tu as donnée est la bonne. X et Y peuvent être égaux, oui, mais en général ils ne le sont pas. Dans ton cas, l'image de f ce sera justement l'ensemble des couples (X,X), qui est un sous-ensemble de P(E)², mais qui n'est pas égal à P(E)².

[Stanley]

Ah je crois avoir compris :
Dans le cas ou X=Y, (X,X) admet un antécédent par f dans P(E), mais c'est qu'un cas particulier, et en génral X est différent de Y et donc (X,Y) n'admet pas forcément d'antécédent par f dans P(E), donc la fonction n'est pas surjective. C'est bien ca ?

[Skullkid]

Exactement.

[Stanley]

Merci beaucoup à vous deux pour votre aide et au plaisir :)