Produit tensoriel

[Archytas]

Salut, je comprends pas du tout ce que c'est qu'un produit tensoriel d'espaces vectoriel. Je sais que c'est un espace vectoriel mais on le définit comme le quotient des combinaison linéaires de ExF par l'espace engendré par les (x+y,z) - (x,z) - (y,z) , (x,y+z)-(x,y) - (x,z), k(x,y) - (kx,y)...
Sauf que pour moi sauf erreur (x+y,z)-(x,z)-(x,y) = (0,-z) et l'autre (-x,0) donc l'espace engendré est ExF ? Pourquoi on s'emmerde avec ces saloperies ?
Et donc E tenseur F = K^(ExF) / ExF = {K^(ExF)} ??????
:help: :help: :help:

[Ben314]

Salut,
Lorsque tu parle des "combinaisons linéaires d'éléments de ExF", ça ne veut... pas dire grand chose... (et ce que ça risque de vouloir dire, ben c'est pas ça...)
Pour définir le produit tensoriel, on part de (l'énorme) e.v. (si E et F sont des e.v. sur K) qui correspond à l'ensemble des "suites" avec .
On commence par considérer le s.e.v. G formé des éléments dont toutes les composantes sont nulles sauf un nombre fini et, pour alléger l'écriture, l'élément où tout les sont nuls sauf un certain est noté .
Je met exprès des crochet et pas des parenthèse pour bien te faire comprendre que ce n'est pas le vecteur de 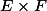mais un autre "objet" d'un autre espace vectoriel.
Partant de là, par définition même de G, les différents forment une base de l'espace G en question : tout élément de G s'écrit, de façon unique comme combinaison linéaire des .

Si tu as bien tout compris, tu devrais comprendre que, par exemple,
- [0,0] n'est pas l'élément neutre de G (un vecteur faisant parti de la base ne peut être nul)
- [x,y+y'] n'est pas égal [x,y]+[x,y']. (la somme de deux vecteurs de la base ne peut pas être un élément de la base)
- a.[x,y] n'est pas égal [ax,ay] ni a [ax,y], ni a [x,ay] sauf si a=1 (si on multiplie un vecteur de la base par a différent de 1, ça ne peut pas faire un autre vecteur de la base)

Bilan, pour le moment, la seule règle de calcul valable dans cet ensemble, c'est

[Archytas]

D'abord merci pour ta réponse mais je saurais pas te dire si c'est plus clair maintenant...
Bon je vais essayer de décortiquer tout ça, tu peux me dire si c'est bon ?
Déjà K^ExF tu les appelles suites mais c'est bien l'ensemble des fonctions de ExF dans K ?
Dans le cours on avait mis des parenthèses : K^(ExF) c'est bien l'ensemble des familles finies (k) indexé par une famille finie d'éléments de ExF ? (déjà merci pour ce point dans ma tête je voyais combinaisons linéaires d'éléments de ExF, j'étais dans les choux). Ok et donc ton élément L vaut 0 partout sauf en un point de ExF ! Très bien !
Juste un truc ce que t'appelle c'est bien et c'est quoi dans ce cas l'élément neutre de G ?
Parce que plus bas dans le cours on dit bien qu'il y a linéarité et tout le bordel des espaces vectoriels !?

[Archytas]

Svp quelqu'un pourrait m'expliquer aussi la définition de mon cours :cry: ? C'est quoi cet espace vectoriel engendré par ces trucs bizarres ?? Je pense que je pourrais m'en sortir si on arrivait juste à m'expliquer par quoi on quotiente K^(ExF) :mur: ! Il doit forcément y avoir une erreur dans mon cours mais tout le monde a la même et je ne trouve aucune définition de ce type sur internet, mon prof a un don pour donner des définitions "exotiques" et c'est loin d'être la première sur laquelle je me casse les dents...

[mathelot]

c'est très simple et expliqué dans tous les livres. Grosso modo, le produit tensoriel
vérifie une propriété universelle dans la catégorie des A-modules ou ds celle des K-espaces vectoriels,
il permet, en factorisant une application, de rendre linéaire une flèche, qui, a priori, était bilinéaire.
comme je n'ai pas étudié tout ça, je ne peux être plus précis. Après, pour utilisation,
on écrit des combinaisons de vecteurs de base du produit tensoriel, et y a qu'à voir les propriétés
des vecteurs de base (qui n'ont p-e pas de propriété,
sauf d'exister) pour fournir une base et augmenter ( par produit) les dimensions des deux espaces initiaux:
Le produit tensoriel agit essentiellement sur les dimensions des e.v pour que

ici

[Ben314]

Déjà K^ExF tu les appelles suites mais c'est bien l'ensemble des fonctions de ExF dans K ?
Dans le cours on avait mis des parenthèses : K^(ExF) c'est bien l'ensemble des familles finies (k) indexé par une famille finie d'éléments de ExF ?
ce t'appelle c'est bien et c'est quoi dans ce cas l'élément neutre de G ?
Parce que plus bas dans le cours on dit bien qu'il y a linéarité et tout le bordel des espaces vectoriels !?

- L'ensemble des applications (quelconques) de A dans B et l'ensemble des suites d'éléments de B indexés par les éléments de A, c'est exactement la même chose via "fonction f" "suite ".
- Effectivement, ce que j'ai appelé G dans le post précédent, est en général noté et si tu veut le voir en terme de fonction, c'est les fonction f:ExF->K nulle partout sauf sur un nombre fini de points.
- Ce que je note [xo,yo], c'est la fonction de ExF->K nulle partout sauf en (xo,yo) où elle vaut 1, et ce n'est pas la même chose que qui est l'image de [xo,yo] par la surjection canonique dans le quotient K^(ExF)/H où H est le s.e.v. de K^(ExF) engendré par les trucs dont tu parle dans ton premier post (et K^(ExF)/H est par définition le produit tensoriel de E avec F)
Par exemple, alors que car est dans le s.e.v. H par lequel on quotiente donc son image dans K^(ExF)/H est nulle.
La différence entre et est exactement la même que celle entre et
- Le neutre de K^(ExF), c'est la fonction identiquement nulle de ExF->K qui n'est évidement pas égale à [0,0] qui est la fonction de ExF->K nulle partout sauf en (0,0) où elle vaut 1.
Dans le produit tensoriel de E par F, c'est à dire dans K^(ExF)/H, l'élément neutre est la classe de la fonction identiquement nulle qui est la même que la classe de [0,0] car [0,0] est dans H donc est bien l'élément neutre du produit tensoriel.
- "il y a linéarité et tout le bordel des espaces vectoriels" dans le quotient K^(ExF)/H et cela tient a la nature du H par lequel on a quotienté : en fait, on a quotienté dans le but de rendre vrai des relations qui ne sont pas vrai dans K^(ExF) exactement comme on quotiente Z par 5Z de façon à rendre vraie la relation 5=0 qui n'est pas vraie dans Z.

[Archytas]

Ok !!! Donc le machin par lequel on quotiente c'est pas des éléments de ExF mais bien de K^(ExF) !?
Et c'est l'espace vectoriel engendré par [x+y,z]-[x,z]-[y,z] et pas (x+y,z) - (x,z) - (y,z) ! Avec [x+y,z]-[x,z]-[y,z] qui vaut l'application qui à quand (x',y') n'est pas (x+y,z) ni (x,z) ni (y,z) et 1 en (x+y,z), -1 en (x,z) et -1 en (y,z) ?! Je comprenais pas comment il était possible de faire la somme de Minkowski d'éléments de ExF avec K^(ExF) (ce qui aurait été les éléments de K^(ExF)/ExF ! Bon c'est toujours pas méga clair mais c'est parce que la machine est costaude mais au moins ça à du sens maintenant, mille merci(s) à vous :jap:

[barbu23]

Bravo @Ben314. :lol3:
Moi aussi, ça n'était pas vraiment claire pour moi, cette façon de construire le produit tensoriel. Très belle explication de ta part @Ben314. :happy3:

[Ben314]

Tout le "fatras" en question, c'est la preuve théorique de l'existence du produit tensoriel et dans pas mal de contexte, (mais pas tous) on s'en fout un peu vu que le bilan final, c'est qu'on a construit un e.v. qui a pour base les où les forment une base de E et les forment une base de F (donc, en dimension finie, la dimension du produit tensoriel de E et F, c'est le produit des dimensions).

[mathelot]

on notera qque le produit tensoriel est excessivement importaant en physqiue
(tenseur de Ricci, pb de courbure,géodésiques)

[Archytas]

Donc je m'en servirai jamais. cqfd :ptdr:
Ou pour linéariser une bête bestiole multilinéaire sans perdre d'infos :king:

[Ben314]

Le produit tensoriel, c'est aussi extrèmement utile en math dans des tonnes de domaines.
Ne serait ce qu'un exemple (parmi... des tas d'autres...) lorsque tu as un K-e.v. E sur un certain corps K, et un surcorps L de K (par exemple C "au dessus" de R ou R "au dessus" de Q) ça te permet en claquant des doigts de fabriquer un L-e.v. E' qui est un prolongement "naturel" du K-e.v. E de départ (tu fait le produit tensoriel de E avec L qui sont tout les deux des K-e.v.)
Si un jour tu manipule les modules, idem : un A-Module M sur un anneau intègre A et hop, un petit coup de produit tensoriel et ça te fabrique un tout beau tout chaud e.v. M' sur le corps des fractions de A qui "prolonge" (plus ou moins...) naturellement le module M (tu y perd tout ce qui a "de la torsion")
Tout ça pour (re)dire que c'est un outil très puissant, et... très utile...

[Archytas]

Ok je prends note que ça peut être cool ! Enfin pour le moment j'en suis au stade ou j'essaie d'imaginer la gueule des vecteurs du quotient et le rapport entre ces vecteurs et la propriété universelle ! Et ça fait quoi le produit tensoriel de K par E ? On a vu en cours que c'est isomorphe à E mais ça sert à quelque chose ?

[Ben314]

Si E est déjà au départ un K-e.v. alors effectivement, c'est comme "de p... dans un violon".
Mais si par exemple E est un Q-e.v. et que tu en fait le produit tensoriel avec R, alors, non seulement ton produit tensoriel sera un Q-e.v. mais ça sera aussi un R e.v. :
Les éléments de ton produit tensoriel seront des sommes finis de truc du style ave et 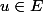et, pour tout réel tu pose (par définition) et c'est pas la peine d'être bien malin pour se douter qu'avec ça tu as un R-e.v.

[Archytas]

Si E est déjà au départ un K-e.v. alors effectivement, c'est comme "de p... dans un violon".
Mais si par exemple E est un Q-e.v. et que tu en fait le produit tensoriel avec R, alors, non seulement ton produit tensoriel sera un Q-e.v. mais ça sera aussi un R e.v. :
Les éléments de ton produit tensoriel seront des sommes finis de truc du style ave et et, pour tout réel tu pose (par définition) et c'est pas la peine d'être bien malin pour se douter qu'avec ça tu as un R-e.v.

Ok ouais c'est badasse . Je garde ça dans un coin de ma tête ! Merci et bonne continuation !