Produit de Cauchy série entière

[mehdi-128]

Bonsoir,

Je veux réaliser le produit de Cauchy des 2 séries entière suivante de rayon de convergence 1 donc pour tout t dans ]-1,1[ :




Le produit de cauchy a pour terme général :

Mais j'ai un problème en 0 que faire ? Que vaut ?

[zygomatique]

salut

il faudrait arrêter d'appliquer bêtement des formules : si les deux séries commencent à 1 on effectue le produit de Cauchy en commençant à 1

d'autre part les deux séries s'annulent en 0 ...

[mehdi-128]

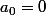
Donc en gros ça veut dire que si la série des an commence à 1 on considère que donc ?

Donc :

[Ben314]

Salut,
"En gros" (comme tu dit), ce qu'on fait, c'est tout bêtement de développer (en considérant qu'on a le droit).
Si tu développe le produit (qui correspond à ton énoncé) :

ça donne quoi ?
Plus précisément,
- C'est quoi la plus petite puissance de t qui apparait ? Avec quel coefficient ?
- Et la puissance suivante, c'est quoi le coeff. ?