Problème de transport d'eau

[Anonyme]

Bonsoir,
Pourriez-vous m'aider à résoudre ce problème, s'il vous plait?

De combien de manières peut-on transporter n litres d'eau en utilisant des bouteilles de 1 et de 2 litres d'eau ?

Répondre à cette question après avoir suivi les étapes suivantes :
a. montrer que l'ensemble des suites x(n) satisfaisant
x(n)=x(n-1)+x(n-2) est un espace vectoriel réel V et calculer sa dimension

b. trouver toutes les suites géométriques dans V et montrer qu'elles forment une base de V

c. Répondre à la question pour n=1 et n=2 et déduire des points précédents la réponse pour n litres

J'ai déjà répondu à la partie a. de cette question mais, en ce qui concerne le reste, je sèche complètement.

Merci d'avance de votre aide.

[Pythales]

Connais-tu la suite de Fibonacci ?

[Anonyme]

euh non désolé...

[Pythales]

La suite de Fibonacci est définie par la relation de récurrence que tu cites. Elle se confond, pour n assez grand, avec une suite géométrique de raison 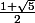qui s'appelle le nombre d'or.
Si on pose et on vérifie que r est solution de l'équation dont une racine est le nombre d'or, l'autre valant 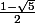. Cette deuxième suite géométrique tend rapidement vers zéro.
Pour répondre à la question :
L'espace vectoriel est de dimension 2
est combinaison linéaire des 2 suites géométriques.