Théorème de transport

[euclide]

Bonjour,

Je cherche une démonstration du résultat suivant. On considère un volume qui dépend donc du temps . On suppose de plus que ce volume se déplace à la vitesse . Enfin on considère un champ scalaire qui dépend aussi temps. Alors on a la relation :



Avec le vecteur normal unitaire sortant du volume et le contour du volume. La difficulté vient du fait que le volume varie en fonction du temps et se déplace, dans le cas contraire on a et on passe alors simplement la dérivée temporelle sous l'intégrale. Mais en prenant en compte le phénomène d'advection du volume... je ne vois pas vraiment comment le démontrer.

Si quelqu'un a une idée, je suis preneur ! Merci bien.

[Doraki]

Le temps fait bouger l'intégrale de deux manières :
- en faisant bouger f
- en faisant bouger le domaine.

Tu y verras plus clair si tu sépares ces deux dépendances :

Regarde une fonction F(t1,t2) = intégrale sur Oméga(t1) de f(x,y,z,t2).

dF/dt2 correspond au terme de gauche.
dF/dt1 correspond au terme de droite, et c'est lui que tu dois étudier.
L'avantage de faire cette décomposition c'est d'avoir que quand tu dérives par rapport à t1, f ne dépend pas de t1.

Après soit tu as un truc du cours qui te donne le terme de droite, soit tu le redémontres.

[euclide]

Merci pour cette idée, si j'ai bien compris, tu proposes les calculs suivants :

(i) On pose d'abord :


(ii) Puis on utilise la formule de dérivation totale :


(iii) On a clairement d'une part : ce qui est bien la première partie du résultat recherché.

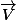
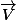
(iv) Ensuite il faut calculer le terme . Pour ce terme, dans le cas où est constant il n'y a pas de problème, j'ai essayé, en revenant à la définition et avec un petit changement de variable (vu que dans ce cas le volume est juste translaté), on peut rapidement trouver le résultat. Mais qu'en est-il dans le cas où est un champ de vitesse (non constant) dépendant aussi du temps ?

Si quelqu'un a une idée pour démontrer ça de façon rigoureuse, ça m'intéresse.