Problème proba
29 messages
- Page 1 sur 2 - 1, 2
Problème proba
Bonjour à tous,
Je suis prof de lettres et en ce moment je cherche à prouver un phénomène stylistique par les stats et les probas. Mais comme je n'y connais pas grand chose (à part ce que j'ai pu étudier par moi-même dans un manuel de statistique linguistique), je galère un peu. Voilà le problème: dans un poème de 21286 vers, il y a 1720 vers de quatre mots et j'ai l'impression que ce type de vers est utilisé en rafales, c'est-à-dire de manière complètement irrégulière. Pour prouver que cela n'est pas dû au hasard, j'ai suivi la méthode du bouquin dont je parlais, à savoir découper le poème en tranches égales (de plus en plus petites pour voir à quel niveau se produit le phénomène : j'ai pris n=100, n=50, n=30, n=15, n=10, n=5 puis n=2), compter le nombre de tranches qui ont 0, 1, 2, 3, ..., 100 vers de quatre mots et comparer cette répartition observée avec la répartition théorique. Or je ne sais pas s'il faut calculer l'effectif théorique selon la loi normale, la loi binomiale ou la loi de Poisson. Là dessus le manuel que j'utilise est assez flottant. Est-ce que vous pourriez m'apporter quelques éclaircissements à ce sujet ? Merci d'avance pour votre aide. Je suis bien sûr à votre disposition si vous avez vous-mêmes besoin que je précise quelque chose (j'espère que tout est clair).
Je suis prof de lettres et en ce moment je cherche à prouver un phénomène stylistique par les stats et les probas. Mais comme je n'y connais pas grand chose (à part ce que j'ai pu étudier par moi-même dans un manuel de statistique linguistique), je galère un peu. Voilà le problème: dans un poème de 21286 vers, il y a 1720 vers de quatre mots et j'ai l'impression que ce type de vers est utilisé en rafales, c'est-à-dire de manière complètement irrégulière. Pour prouver que cela n'est pas dû au hasard, j'ai suivi la méthode du bouquin dont je parlais, à savoir découper le poème en tranches égales (de plus en plus petites pour voir à quel niveau se produit le phénomène : j'ai pris n=100, n=50, n=30, n=15, n=10, n=5 puis n=2), compter le nombre de tranches qui ont 0, 1, 2, 3, ..., 100 vers de quatre mots et comparer cette répartition observée avec la répartition théorique. Or je ne sais pas s'il faut calculer l'effectif théorique selon la loi normale, la loi binomiale ou la loi de Poisson. Là dessus le manuel que j'utilise est assez flottant. Est-ce que vous pourriez m'apporter quelques éclaircissements à ce sujet ? Merci d'avance pour votre aide. Je suis bien sûr à votre disposition si vous avez vous-mêmes besoin que je précise quelque chose (j'espère que tout est clair).
Voilà d'ailleurs le tableau que j'obtiens pour n=100 (la colonne de droite donne le nombre de vers de quatre mots par tranches et celle de gauche le nombre de tranches concernées):
3- 22
4 17
5 10
6 23
7 25
8 21
9 19
10 26
11 13
12 11
13 10
14+ 15
Total 212
J'ai aussi oublié de préciser que p=0,081.
Merci d'avance,
Maldoror
3- 22
4 17
5 10
6 23
7 25
8 21
9 19
10 26
11 13
12 11
13 10
14+ 15
Total 212
J'ai aussi oublié de préciser que p=0,081.
Merci d'avance,
Maldoror
bonjour,
Pour compléter ce qu'a écrit nuage, avec des tranches de 100 et une moyenne par tranche égale à 8, la loi binomiale peut s'approcher par la loi de Poisson ou la loi normale. Donc le choix ne changera pas les résultats.
Par ailleurs, j'ai regardé tes données : c'est très loin d'une distribution aléatoire et un peu plus près d'une distribution uniforme.
Pour compléter ce qu'a écrit nuage, avec des tranches de 100 et une moyenne par tranche égale à 8, la loi binomiale peut s'approcher par la loi de Poisson ou la loi normale. Donc le choix ne changera pas les résultats.
Par ailleurs, j'ai regardé tes données : c'est très loin d'une distribution aléatoire et un peu plus près d'une distribution uniforme.
Merci à tous les deux ! Mais il y a encore quelque chose qui me chagrine. À vrai dire, Alben met le doigt sur ce qui me pose problème : je n'arrive pas à comprendre pourquoi approcher la loi binomiale par une loi de poisson ou une loi normale et pourquoi ne pas calculer directement la répartition théorique selon la loi binomiale... De plus, avant de poser la question sur le forum j'ai fait les calculs selon les trois lois, puis appliquer le test du Khi2 et je n'obtiens pas du tout les mêmes résultats dans les trois cas. Dernier point, Alben, que veux-tu dire par "uniforme" ?
En tout cas, merci beaucoup pour vos réponses.
Maldoror
En tout cas, merci beaucoup pour vos réponses.
Maldoror
J'ai aussi calculé selon les trois lois et je trouve comme khi deux
binomiale =59
poisson=43
normale=53
Comme avec moins d'une quinzaine de résultats il est pratiquement impossible de dépasser un khi² de 10, cela revient donc au même. D'ailleurs les effectifs théoriques sont voisins à une ou deux unités près.
J'ai aussi calculé le khi² pour une distribution uniforme, ça donne 21 ce qui est encore trop mais plus plausible.
Par distribution uniforme, je veux dire que les tranches contiendraient un nombre presque égal de vers à 4 mots. En d'autres termes, l'auteur s'arrangerait pour qu'il y ait à peu près la même proportion de vers à 4 mots dans toutes les parties de son oeuvre. En gros, il ferait des rattrapages ("voilà pas mal de temps que je n'en ai pas utilisé, il faut en introduire...")
PS Son rythme d'appréciation n'étant surement pas tous les 100 vers, cela explique que ça ne marche pas parfaitement. En outre ce rythme n'est sans doute pas constant.
PS2 Tu as parlé de rafales. Pour moi, ça évoque des séquences comportant un nombre élevé de vers à 4 mots puis très peu pendant un certain temps et encore une rafale etc...
Si l'usage de ce type de vers correspond à quelques chose de précis (littéraire ou psychologique), on pourrait relier ces rafales à un rythme littéraire ou psy...
binomiale =59
poisson=43
normale=53
Comme avec moins d'une quinzaine de résultats il est pratiquement impossible de dépasser un khi² de 10, cela revient donc au même. D'ailleurs les effectifs théoriques sont voisins à une ou deux unités près.
J'ai aussi calculé le khi² pour une distribution uniforme, ça donne 21 ce qui est encore trop mais plus plausible.
Par distribution uniforme, je veux dire que les tranches contiendraient un nombre presque égal de vers à 4 mots. En d'autres termes, l'auteur s'arrangerait pour qu'il y ait à peu près la même proportion de vers à 4 mots dans toutes les parties de son oeuvre. En gros, il ferait des rattrapages ("voilà pas mal de temps que je n'en ai pas utilisé, il faut en introduire...")
PS Son rythme d'appréciation n'étant surement pas tous les 100 vers, cela explique que ça ne marche pas parfaitement. En outre ce rythme n'est sans doute pas constant.
PS2 Tu as parlé de rafales. Pour moi, ça évoque des séquences comportant un nombre élevé de vers à 4 mots puis très peu pendant un certain temps et encore une rafale etc...
Si l'usage de ce type de vers correspond à quelques chose de précis (littéraire ou psychologique), on pourrait relier ces rafales à un rythme littéraire ou psy...
Autant pour moi : je trouvais le même Khi2 que toi pour la loi binomiale et la loi de poisson, mais pas pour la loi normale. Mais je viens de trouver mon erreur : j'utilisais la variance expérimentale et non la variance théorique et trouvais du coup des données théoriques très proches de la répartition observée.
Bon mais j'ai encore quelques questions si cela ne vous dérange pas :
1° j'ai bien compris maintenant qu'on peut approcher la loi binomiale par les deux autres, mais comme je dois publier mes résultats de manière très simple (c'est-à-dire sans présenter les résultats par les trois lois), mais que je ne voudrais pas non plus qu'un statisticien tatillon cherche la petite bête, laquelle des lois je dois utiliser légitimement ?
2° j'aimerais aussi savoir dans quel cas je suis si je fais varier n (dans l'idée de voir si le phénomène de concentration se produit à grande ou à petite échelle). J'ai toutes les données pour n=50, 30, 15, 10, 5 et 2. Qu'en pensez-vous ?
3° Alben, c'est exactement ce que j'entendais par rafales : de longs moments sans vers de 4 mots, et tout d'un coup de longs moments avec des concentrations. Mais dis-moi, comment as-tu réalisé ton Khi2 (qui te donne un résultat différent) pour tester l'uniformité ? Tu m'as bien intrigué...
Merci encore à toi ! Tu sauves des mois et des mois de travail.
Maldoror
Bon mais j'ai encore quelques questions si cela ne vous dérange pas :
1° j'ai bien compris maintenant qu'on peut approcher la loi binomiale par les deux autres, mais comme je dois publier mes résultats de manière très simple (c'est-à-dire sans présenter les résultats par les trois lois), mais que je ne voudrais pas non plus qu'un statisticien tatillon cherche la petite bête, laquelle des lois je dois utiliser légitimement ?
2° j'aimerais aussi savoir dans quel cas je suis si je fais varier n (dans l'idée de voir si le phénomène de concentration se produit à grande ou à petite échelle). J'ai toutes les données pour n=50, 30, 15, 10, 5 et 2. Qu'en pensez-vous ?
3° Alben, c'est exactement ce que j'entendais par rafales : de longs moments sans vers de 4 mots, et tout d'un coup de longs moments avec des concentrations. Mais dis-moi, comment as-tu réalisé ton Khi2 (qui te donne un résultat différent) pour tester l'uniformité ? Tu m'as bien intrigué...
Merci encore à toi ! Tu sauves des mois et des mois de travail.
Maldoror
Je précise ma question 1° : comment se fait-il que le Khi2 selon la loi de Poisson soit moins élevé que celui selon la loi binomiale ? Est-ce que ce n'est pas le signe que c'est elle qui donne le meilleur modèle ? Du coup, est-ce que je dois présenter les chiffres théoriques qu'elle me donne, même si normalement je suis dans le cas d'une distribution binomiale ? J'espère que c'est plus clair.
Salut,
Si on a une distribution «au hasard» le modèle théorique est une loi hypergéométrique.
On peut l'approcher par une loi binomiale, et cette approximation s'améliore quand n diminue.
Les autres approximations se dégradent quand n devient «petit».
Dans la mesure où calculer les probabilités suivant une loi binomiale ne pose plus de problèmes pratiques (fonction LOI.BINOMIALE() dans OooCalc ou dans Exel) je te recommande de l'utiliser.
Pour tester l'uniformité tu mets le même nombre de vers de quatre mots dans chaque tranche de n vers.
Je n'ai pas fait les calculs, mais je crois qu'on peut faire confiance à alben. Les modèles loi de Poisson , loi binomiale et loi normale sont à rejeter pour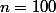 .
.
Il devrait-être possible de déterminer pour avoir une répartition uniforme avec une probabilité raisonnable.
pour avoir une répartition uniforme avec une probabilité raisonnable.
Ps1 : pour utiliser le modèle binomial il est recommandé d'avoir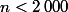 dans ton cas.
dans ton cas.
Ps2 :21 286 vers c'est beaucoup. Serait-il indiscret de te demander quelle uvre tu étudies ?
Si on a une distribution «au hasard» le modèle théorique est une loi hypergéométrique.
On peut l'approcher par une loi binomiale, et cette approximation s'améliore quand n diminue.
Les autres approximations se dégradent quand n devient «petit».
Dans la mesure où calculer les probabilités suivant une loi binomiale ne pose plus de problèmes pratiques (fonction LOI.BINOMIALE() dans OooCalc ou dans Exel) je te recommande de l'utiliser.
Pour tester l'uniformité tu mets le même nombre de vers de quatre mots dans chaque tranche de n vers.
maldoror a écrit:: comment se fait-il que le Khi2 selon la loi de Poisson soit moins élevé que celui selon la loi binomiale ? Est-ce que ce n'est pas le signe que c'est elle qui donne le meilleur modèle ?
Je n'ai pas fait les calculs, mais je crois qu'on peut faire confiance à alben. Les modèles loi de Poisson , loi binomiale et loi normale sont à rejeter pour
Il devrait-être possible de déterminer
Ps1 : pour utiliser le modèle binomial il est recommandé d'avoir
Ps2 :21 286 vers c'est beaucoup. Serait-il indiscret de te demander quelle uvre tu étudies ?
Je rebondis sur ce que tu viens de dire : j'ai aussi calculé l'effectif théorique selon la loi hypergéométrique (en me basant sur un autre bouquin et sans savoir si mon cas se rapprochait du cas traité par l'auteur). Si je comprends bien, les trois autres lois n'offrent qu'une approximation : pourquoi alors je ne présenterai pas les résultats que j'obtiens en comparant la répartition observée avec la répartition théorique calculée selon la loi hypergéométrique ? Bien sûr, cela ne change pas grand chose et j'en suis maintenant conscient : comme l'a dit Alben, les effectifs ne changent que d'une ou deux unités, mais c'est par souci de "perfection".
maldoror a écrit:Ah et sinon je ne comprends pas ce que tu veux dire quand tu dis qu'il serait possible de déterminer n pour avoir une répartition uniforme avec une probabilité raisonnable. Désolé d'être lourd :briques:
Tu ne l'es pas.
En fait il s'agit d'une croyance : pour un découpage en tranches égales, de longueur bien choisie, on doit avoir à peu près le même nombre de vers de quatre mots par tranche. Il faut, bien sur, que les tranches soient assez nombreuses (ie au moins une centaine, compte tenu de l'ampleur de l'uvre).
OK, merci beaucoup. Ça commence à devenir un peu plus clair. J'ai fait mes calculs selon la loi hypergéométrique grâce à l'autre bouquin dont je parlais :
loi hypergéométrique de paramètres T (longueur totale du corpus), t (longueur d'une partie) et f (fréquence totale d'une forme donnée)
à la manière d'excel, prob (x=k) = COMBIN(f;k)*COMBIN(T-f;t-k)/COMBIN(T;t)
Ça te semble correct ? Ça devrait en tout cas, puisque je tombe sur des chiffres très proches de ceux que je trouve avec la loi binomiale, comme tu le disais.
Bon, et donc je peux utiliser la loi hypergéométrique ou la loi binomiale pour mes calculs, même lorsque je fais baisser la valeur de n ? J'espère que je ne donne pas l'impression de poser la même question trente fois, mais ça me permet de vérifier pas à pas que je comprends bien le raisonnement (je vais quand même devoir l'expliquer dans un article).
Ah, j'allais oublier : les 21286 vers que j'ai dépouillés (je te raconte pas l'horreur) sont en fait des vers grecs (je suis prof de lettres classiques). C'est un poème pas connu du tout d'un auteur du 5e s. ap. J.C.
Merci encore les gars, vous me sauvez la vie !
Maldoror
loi hypergéométrique de paramètres T (longueur totale du corpus), t (longueur d'une partie) et f (fréquence totale d'une forme donnée)
à la manière d'excel, prob (x=k) = COMBIN(f;k)*COMBIN(T-f;t-k)/COMBIN(T;t)
Ça te semble correct ? Ça devrait en tout cas, puisque je tombe sur des chiffres très proches de ceux que je trouve avec la loi binomiale, comme tu le disais.
Bon, et donc je peux utiliser la loi hypergéométrique ou la loi binomiale pour mes calculs, même lorsque je fais baisser la valeur de n ? J'espère que je ne donne pas l'impression de poser la même question trente fois, mais ça me permet de vérifier pas à pas que je comprends bien le raisonnement (je vais quand même devoir l'expliquer dans un article).
Ah, j'allais oublier : les 21286 vers que j'ai dépouillés (je te raconte pas l'horreur) sont en fait des vers grecs (je suis prof de lettres classiques). C'est un poème pas connu du tout d'un auteur du 5e s. ap. J.C.
Merci encore les gars, vous me sauvez la vie !
Maldoror
maldoror a écrit:OK, merci beaucoup. Ça commence à devenir un peu plus clair. J'ai fait mes calculs selon la loi hypergéométrique grâce à l'autre bouquin dont je parlais :
loi hypergéométrique de paramètres T (longueur totale du corpus), t (longueur d'une partie) et f (fréquence totale d'une forme donnée)
à la manière d'excel, prob (x=k) = COMBIN(f;k)*COMBIN(T-f;t-k)/COMBIN(T;t)
Ça te semble correct ?
C'est correct.
maldoror a écrit:Bon, et donc je peux utiliser la loi hypergéométrique ou la loi binomiale pour mes calculs, même lorsque je fais baisser la valeur de n ?
L'approximation de la loi hypergéométrique par la loi binomiale s'améliore quand n diminue.
Ps : C'est dommage, mais ma connaissance de la littérature grecque ancienne ne dépasse pas les grands classiques. Et, en particulier, j'ignore tout de ce qui se passe après JC.
Puisque tu as les moyens de calculer directement par la loi binomiale, pas la peine de chercher des approximationsmaldoror a écrit:1° j'ai bien compris maintenant qu'on peut approcher la loi binomiale par les deux autres, mais comme je dois publier mes résultats de manière très simple (c'est-à-dire sans présenter les résultats par les trois lois), mais que je ne voudrais pas non plus qu'un statisticien tatillon cherche la petite bête, laquelle des lois je dois utiliser légitimement ?
Il y a deux questions :maldoror a écrit:3° Alben, c'est exactement ce que j'entendais par rafales : de longs moments sans vers de 4 mots, et tout d'un coup de longs moments avec des concentrations. Mais dis-moi, comment as-tu réalisé ton Khi2 (qui te donne un résultat différent) pour tester l'uniformité ? Tu m'as bien intrigué...
1 la répartition uniforme : j'ai supposé que chaque valeur possible était présente dans autant de tranches. Cela ne fournit pas d'info sur la distribution effective des vers à 4 mots mais permet si le khi² avait été inférieur à 10, de supposer l'existence de séquences régulières... Pour le calcul, j'ai simplement pris le rapport 212/12 comme effectif théorique partout.
2 Les rafales : l'utilisation d'un test de khi² mélange toutes les données et le rythme auquel ces vers apparaissent dans le texte n'est plus perceptible.
Pour mettre en évidence celui-ci, j'adopterais une démarche différente consistant à attribuer à chaque vers à 4 mots l'ordre dans lequel il figure dans l'ouvrage complet.
Par exemple 1er vers à 4 mots= vers N° 60, 2ième->62 .....220ième->21235
et ensuite travailler sur les différences (distances) Il existe, je crois, des méthodes pour cela
Je suis pas sûr de comprendre là, Alben. J'ai peur que tu n'aies pas compris le premier tableau que j'ai donné : je l'avais simplifié en prévision du khi2 pour ne pas avoir d'effectif théorique inférieur à 5 ; les première et dernière lignes signifient donc "inférieur ou égal à 3" (3-) et "supérieur ou égal à 14" (14+). (J'avoue que ce n'était pas clair, désolé). C'est pour ça que j'ai douze lignes de données et, j'imagine, que tu divisais par 12, mais en fait dans mes observations, j'ai des données pour 20 des 100 lignes que comprend mon tableau étendu. Du coup, pour tester l'uniformité, on doit mettre un effectif de 212/100 dans les 100 lignes, non ?
Sinon, les résultats des tests de khi2 que j'ai pratiqués pour différentes valeurs de n ne permettent plus de rejeter l'hypothèse nulle d'une répartition aléatoire à partir de n=5. Ce n'est pas suffisant pour prouver que les concentrations ne se font pas à si petite échelle ?
Je demande ça, mais en fait pour dire la vérité j'ai aussi effectué la méthode que tu indiquais, et ce de deux manières : d'abord en ne considérant que les intervalles entre chaque vers de 4 mots, puis en considérant en plus des intervalles les écarts entre deux intervalles successifs (test des différences quadratiques moyennes successives, il me semble). Mais d'après les manuels que je suis, les résultats que j'obtiens me permettent de prouver que la répartition est irrégulière, mais pas de voir à quelle échelle le phénomène se produit.
Merci de me consacrer votre temps :we:
Sinon, les résultats des tests de khi2 que j'ai pratiqués pour différentes valeurs de n ne permettent plus de rejeter l'hypothèse nulle d'une répartition aléatoire à partir de n=5. Ce n'est pas suffisant pour prouver que les concentrations ne se font pas à si petite échelle ?
Je demande ça, mais en fait pour dire la vérité j'ai aussi effectué la méthode que tu indiquais, et ce de deux manières : d'abord en ne considérant que les intervalles entre chaque vers de 4 mots, puis en considérant en plus des intervalles les écarts entre deux intervalles successifs (test des différences quadratiques moyennes successives, il me semble). Mais d'après les manuels que je suis, les résultats que j'obtiens me permettent de prouver que la répartition est irrégulière, mais pas de voir à quelle échelle le phénomène se produit.
Merci de me consacrer votre temps :we:
Si je peux me permettre un avis non autorisé, sur la base de mon imparfaite connaissance de la littérature française.
Hors cas de formes genre sonnets les échelles avec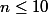 me semblent peu pertinentes.
me semblent peu pertinentes.
Mais je me trompe peut-être (mes connaissances théoriques dans ce domaine sont à peu près nulles).
Pour tester une répartition uniforme (et donc non aléatoire) des vers de quatre mots, je regarderais plutôt les subdivisions fournie par l'auteur. En les divisant éventuellement en sous parties contenant approximativement le même nombre de vers. Et plutôt pour des valeurs de supérieures à 100.
supérieures à 100.
Hors cas de formes genre sonnets les échelles avec
Mais je me trompe peut-être (mes connaissances théoriques dans ce domaine sont à peu près nulles).
Pour tester une répartition uniforme (et donc non aléatoire) des vers de quatre mots, je regarderais plutôt les subdivisions fournie par l'auteur. En les divisant éventuellement en sous parties contenant approximativement le même nombre de vers. Et plutôt pour des valeurs de
Je vais essayer de m'expliquer un peu mieux : si je voulais faire varier n jusqu'à n=5 ou n=2, c'est pour voir si la répartition irrégulière des formes marquées "tolère" des intervalles longs ou courts. Comme à partir de n=5, le khi2 n'est plus concluant, je me disais que cela voulait dire que les concentrations exceptionnelles ne se font jamais avec des passages où tout d'un coup tous les vers ne comportent que 4 mots, mais plutôt avec des passages à forte teneur en vers marqués, mais où on trouve tout de même des "respirations". Je ne sais pas si je me fais bien comprendre. Mais en tout cas, merci pour ton avis tout à fait pertinent, Nuage.
En ce qui concerne ce que tu me conseilles pour tester d'uniformité, ce que j'ai à disposition, c'est des subdivisions en chants (48 chants de longueur très très inégale). J'ai d'ailleurs aussi effectué un test du khi2 sur la répartition en fragments (chants) et non en tranches (100 vers) et le résultat est très concluant (163 pour 47 ddl). Mais pour tester l'uniformité par chant, je ne vois pas trop comment procéder et prendre en compte la différence de longueur des chants.
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
