Problème forme différentielle exacte

[stansoad0108]

Bonjour à tous,

Petit problème sur un exo :
Soit la forme différentielle w(x,y) = (1+2x²y)dx + x^3 dy
Nous avons montré qu'elle n'est pas exacte sur R².

Ensuite nous devons déterminer une fonction réelle d'une variable réelle de Classe C1 sur R, f, telle que w1(x,y) = f(x²y)*w(x,y) soit exacte, et déterminer les primitives de w1.

J'ai commencé comme ceci :

w1(x,y) = f(x²y) ( (1+2x²y)dx + x^3dy)
= f(x²y)(1+2x²y)dx + f(x²y)x^3dy

On sait que w1(x,y) est exacte dc :
f(x²y)(1+2x²y) = df/dx
f(x²y)x^3 = df/dy

A partir de la, je reste bloqué...
Merci d'avance

[Nightmare]

Bonsoir,

Attention, dans tes df/dx et df/dy, ce n'est pas le même f !

Il nous faut trouver une application F telle que

[peedro]

Oui désolé pour l'écriture, mais je le sous-entendais... :happy2:

[stansoad0108]

Oui désolé pour l'écriture...je l'avais sous-entendu :we:

[Nightmare]

D'accord,

ce que je ferai : je résoudrai les équation partielles en fonction d'une primitive de f et je choisirai f pour qu'on retrouve la même chose dans les deux résultats.

En l'occurrence lorsqu'on va intégrer, un changement de variable du style va nous permettre de se ramener dans les deux cas à notre primitive de f.

[Nightmare]

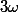
Ou sinon, je chercherai f pour que soit fermée (ce qui est plus simple) et vu que R² est étoilé, Poincaré nous permettra de conclure.

[stansoad0108]

D'accord merci !

Mais quand je veux intégrer le système,

f(t)(1+2x²y) = dF/dx
et
f(t)*x^3 = dF/dy

j'intègre la deuxième équation (plus simple) : F(x,y) = x^3F(t) + Cst(x)
Mais je ne suis même pas sur de ce résultat
De plus je ne vois pas comment intégrer la première équation...

[Nightmare]

Oula, le changement de variable est un peu hâtif pour le coup ! Il faut d'abord faire apparaître les intégrales ! Mais comme je t'ai dit, la méthode de trouver d'abord f pour que w soit fermée est plus rapide.

[stansoad0108]

Pour ta méthode de w fermée et avec R² est étoilé, Poincaré nous permettra de conclure.
Je n'ai jamais entendu parlé de ce théorème...

Sinon je vais essayer avec la première méthode ; je reposterai si je n'y arrive pas

Merci encore

[Nightmare]

Le théorème de Poincaré te dit qu'une forme différentielle fermée sur un ouvert étoilé est exacte.

[stansoad0108]

Euuuh ouvert étoilé, jamais vu...
Juste vu un ouvert simplement connexe...

Et on nous a mis dans notre cour qu'un fermé n'est pas forcément exacte.

[Nightmare]

une partie étoilée lorsqu'on peut trouver un point A tel que pour tout M de la partie, le segment [AM] est dans la partie.

[Pythales]

Juste une curiosité : pourquoi notes-tu systématiquement et x^3 ?

[Nightmare]

Ce message m'est adressé Pythales?

[Pythales]

Indépendamment de ma question, écris que
en posant soit et et tout se simplifie ...

[Pythales]

Non, Nightmare, il s'adressait à l'auteur de la question...