Salut tout le monde,
Soit E un espace vectoriel normé et U un ensemble fermé de E tel que pour tout x,y dans U, (x+y)/2 est dans U.
Alors U est convexe.
Est-ce que quelqu'un a une idée de preuve autre qu'une décomposition en base 2 ?
Merci d'avance.
@+ Boris.
Un problème de convexité
5 messages
- Page 1 sur 1
Par l'absurde, soient x,y dans U et  dans [0,1] tels que
dans [0,1] tels que
)
Soit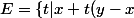 \notin U}) , non vide, minoré par 0, majoré par 1,
, non vide, minoré par 0, majoré par 1,
Soit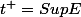 ,
, 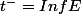
Comme U est un fermé) et
et ) sont dans U.
sont dans U.
On en déduit dès lors que leur milieu a est dans U.
En regardant le milieu de a et de x et le milieu de a et de y (faire un dessin d'un segment), on montre que ne peut qu'être égal à
ne peut qu'être égal à 
Conclure est alors évident.
Soit
Soit
Comme U est un fermé
On en déduit dès lors que leur milieu a est dans U.
En regardant le milieu de a et de x et le milieu de a et de y (faire un dessin d'un segment), on montre que
Conclure est alors évident.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
