Bonjour je suis débutant en math.
J'ai un problème de compréhension sur le théorème de CANTOR.
L'application f(x) = x² de R dans R+ est bien surjective.
R+ est bien une partie de R ce qui contre dit Cantor.
Où est mon erreur dans mon raisonnement? SVP
Problème avec Cantor
7 messages
- Page 1 sur 1
Il vaudrait mieux rappeler de quel théorème de Cantor tu parles. Je suppose qu'il s'agit du suivant :
Théorème : si E est un ensemble, E ne peut être mis en bijection avec l'ensemble de ses parties.
Il n'y a aucune contradiction ; on ne dit pas qu'il n'existe pas de partie de E telle que E ne peut être mis en bijection avec E (c'est trivialement faux : en effet, E EST une partie de E, et l'application identité met donc bien E en bijection avec lui-même...), mais que E ne peut être mis en bijection avec l'ensemble de tous ses sous-ensembles.
Pour contredire le théorème avec R, il faudrait que tu trouves une application qui à tout x réel associe un sous-ensemble de R, et qui soit bijective (ne cherche pas trop, c'est impossible).
Petit exercice pour vérifier que tu as bien compris ce qu'est l'ensemble des parties : quel est l'ensemble des parties de l'ensemble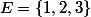 ?
?
Théorème : si E est un ensemble, E ne peut être mis en bijection avec l'ensemble de ses parties.
Il n'y a aucune contradiction ; on ne dit pas qu'il n'existe pas de partie de E telle que E ne peut être mis en bijection avec E (c'est trivialement faux : en effet, E EST une partie de E, et l'application identité met donc bien E en bijection avec lui-même...), mais que E ne peut être mis en bijection avec l'ensemble de tous ses sous-ensembles.
Pour contredire le théorème avec R, il faudrait que tu trouves une application qui à tout x réel associe un sous-ensemble de R, et qui soit bijective (ne cherche pas trop, c'est impossible).
Petit exercice pour vérifier que tu as bien compris ce qu'est l'ensemble des parties : quel est l'ensemble des parties de l'ensemble
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
