bonjour,
je rencontre quelque difficulté à résoudre une question de mon exercice
Une source émet une suite de 8 lettres choisies indépendamment les unes des autres parmi les lettres a, b et c suivant la loi de probabilité suivante :
Lettre a b c
Probabilité 0.37 0.42 0.21
Quelle est la probabilité que, dans une telle suite, la lettre a apparaisse 1 fois ?
La probabilité est 0.11659383
On vous dit que dans la suite de 8 lettres émise par la source, la lettre a apparaît 1 fois. Quelle est la probabilité pour que, dans cette suite, il y ait 6 fois la lettre b et 1 fois la lettre c ?
c'est sur cette question que je n'arrive pas a trouvé le résultat qui est 0.20484682
pourriez vous m'aider s'il vous plait
merci d'avance
Probabilité - séquence aléatoire
6 messages
- Page 1 sur 1
Re: probabilité - séquence aléatoire
Salut,
Perso, je commencerais par dire qu'à chaque tirage, la proba de tirer un b sachant qu'on a pas tiré un a est
(42/100)/(1-(37/100)) = 42/63 = 2/3
et celle tirer un c sachant qu'on a pas tiré un a est
(21/100)/(1-37/100) = 21/63 = 1/3.
Ensuite, sur 7 tirages (8 moins celui avec un le a), la proba d'avoir 6 b et 1 c, ben c'est
binomial(7;1)*(2/3)^6*(1/3) = 7*2^6/3^7 = 448/2187
Perso, je commencerais par dire qu'à chaque tirage, la proba de tirer un b sachant qu'on a pas tiré un a est
(42/100)/(1-(37/100)) = 42/63 = 2/3
et celle tirer un c sachant qu'on a pas tiré un a est
(21/100)/(1-37/100) = 21/63 = 1/3.
Ensuite, sur 7 tirages (8 moins celui avec un le a), la proba d'avoir 6 b et 1 c, ben c'est
binomial(7;1)*(2/3)^6*(1/3) = 7*2^6/3^7 = 448/2187
Modifié en dernier par Ben314 le 13 Mar 2018, 23:46, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilité - séquence aléatoire
merci beaucoup pour cette réponse clair qui me semble évidente, j'ai chercher trop compliqué apparemment
merci
merci
Re: probabilité - séquence aléatoire
j'aimerai savoir ce qui aurait changé si on n'avait pioché deux a au départ, si possible, merci
Re: probabilité - séquence aléatoire
Si, toujours en tirant 8 lettre avec ces proba là, tu cherche la proba de :
tirer "b" et
"b" et  "c" sachant qu'on a tiré
"c" sachant qu'on a tiré  "a" (avec
"a" (avec 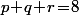 )
)
alors c'est exactement la même chose, à savoir
binomial( p+q ; p ) * (2/3)^p * (1/3)^q
Après, une autre façon d'obtenir le résultat, c'est de raisonner "globalement" en écrivant que
p( tirer "b" et
"b" et  "c" sachant qu'on a tiré
"c" sachant qu'on a tiré  "a" )
"a" )
= p( tirer "b" et
"b" et  "c" et
"c" et  "a" ) / p( tirer
"a" ) / p( tirer  "a" )
"a" )
Le numérateur, c'est^p(0,\!21)^q(0,\!37)^r)
Le dénominateur, c'est!}(0,\!37)^r(1\!-\!0,\!37)^{8-r}=\dfrac{8!}{r!(p\!+\!q)!}(0,\!37)^r(0,\!41\!+\!0,\!21)^{p+q})
ce qui donne bien la même chose qu'avec l'autre méthode, mais ça demande à savoir (où a retrouver) comment se calcule un truc du type p( tirer "b" et
"b" et  "c" et
"c" et  "a" ) qui est une généralisation de la loi binomiale qu'on appelle évidement loi multinomiale (mais on peut parfaitement calculer la valeur de proba. en ayant jamais entendu parler de loi multinomiale)
"a" ) qui est une généralisation de la loi binomiale qu'on appelle évidement loi multinomiale (mais on peut parfaitement calculer la valeur de proba. en ayant jamais entendu parler de loi multinomiale)
tirer
alors c'est exactement la même chose, à savoir
binomial( p+q ; p ) * (2/3)^p * (1/3)^q
Après, une autre façon d'obtenir le résultat, c'est de raisonner "globalement" en écrivant que
p( tirer
= p( tirer
Le numérateur, c'est
Le dénominateur, c'est
ce qui donne bien la même chose qu'avec l'autre méthode, mais ça demande à savoir (où a retrouver) comment se calcule un truc du type p( tirer
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
