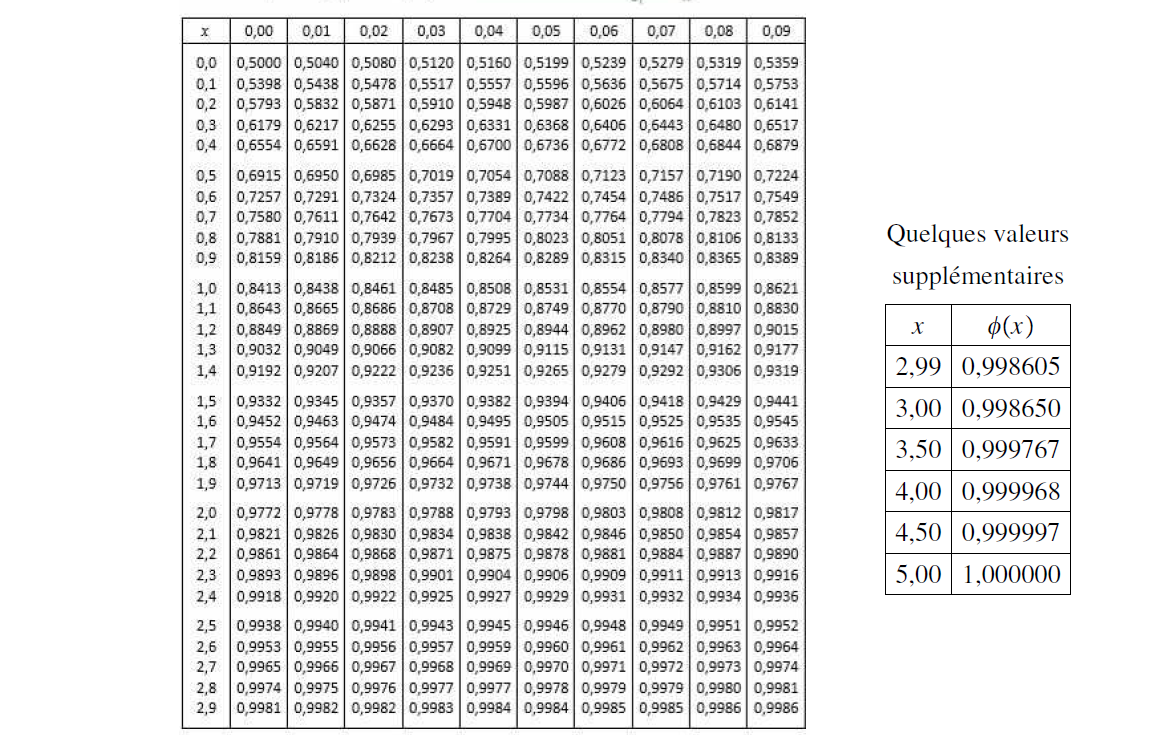
novicemaths a écrit:= P(X \leq)-P(X < 0)=\phi(1)-\phi(0) =\phi(1)-(1-\phi(0)) =\phi(1) + (\phi(0) -1) = 0,8413 + 0,500-1 =1,3413 -1 = 0,3413)
C'est juste mathématiquement parlant mais je pense qu'il y a quelque chose qui n'est pas clair pour toi. Il n'y a aucun besoin de passer par le complémentaire et si tu le fais systématiquement, ce sera faux en dehors du cas particulier 0,500. L'interet d'utiliser la formule
=1-\phi(x))
qui se justifie par
=1-P(X >-x)=1-P(X<x))
est de pouvoir lire la table même pour des valeurs négatives. Mais si on a une valeur positive (ou 0), il n'y a rien à faire, on peut lire directement la table
=\phi(1)-\phi(0) = 0,8413 - 0,5000 = 0,3413)
novicemaths a écrit:= \phi(1) - \phi(-2) = \phi(1) - (1-\phi(2)) = \phi(1) +\phi(2) -1 = 0,8413 +0,9772 -1 = 1,8185 -1 =0,8185)
Parfait
novicemaths a écrit: = 0,975 \Longleftrightarrow P(X \leq 1,96 )= 0,975)
Pour ci-dessous, je ne pense pas que c'est la bonne méthode.

Effectivement, ce que tu écris n'a pas beaucoup de sens. Je pense que tu ne comprends pas la question, on te demande précédemment de résoudre
 = 0,975)
, avec X qui suit une loi N(0,1). Tu sais dans ce cas que
= 0,975)
alors tu peux en déduire que la solution est
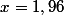
.
Maintenant dans le cas d'une variable X qui suit une loi N(4,2), tu dois à nouveau résoudre
 = 0,975)
. Il faut commencer par centrer réduire donc
 = 0,975)
avec
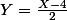
qui suit une loi N(0,1). On reprend comme précédemment et donc que vaut
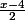
à ton avis ?