Bonjour, voici un exercice de probabilité. Je suis bloquée à la question N°3, pouvez vous me donner des indices, je ne sais vraiment pas comment my prendre.
Je remercie davance tous ceux qui prendront du temps pour maider.
1ère partie : énoncé de lexercice
2ème partie : mes réponses
Dans un certain pays, 15 % de la population est contaminée par le virus du sida. On met en place une stratégie de dépistage par un test biologique qui est négatif lorsque le sujet est sain, et positif lorsque le sujet est contaminé. On néglige les risques derreur du test.
1) Une campagne de dépistage est mise en place sur un échantillon de 500 personnes prises au hasard dans la population. Sous quelles conditions peut-on assimiler cet échantillon à un tirage avec remise ?
2) On appelle X la variable aléatoire donnant le nombre de tests positifs sur léchantillon de 500 personnes. Quelle loi suit cette variable aléatoire ? Quelle est son espérance mathématique et son écart-type ?
3) On appelle E lévénement : « plus de 20% de ces 500 tests sont positifs ». Comment calculer la probabilité de cet événement ? Est-ce humainement possible ? Vous aurez à exposer lapproximation dune loi binomiale par une loi normale (conditions dutilisation, correction de continuité). Utilisez alors ces résultats pour la situation étudiée, et donner une valeur arrondie à 4 décimales de ce nombre.
4) De la même manière, déterminer la probabilité des évènements : E1 : »plus de la moitié de ces 200 tests sont positifs » et E2 « de 10 à 20% de ces tests sont positifs.
REPONSE 1 : La taille de léchantillon est inférieure à 10 % de la population (500 personnes, sur des millions de gens). Donc, on assimile cet échantillon à un tirage avec remise.
REPONSE 2 : Cest la loi Binomiale, de paramètre B(500 ;0.15)
- Son espérance est E (S500) = 500 x 0.15 = 75
- Son écart type est ;) (500) = ;) 500 x 0.15 x 0.85 = 7.98
REPONSE 3 : Il faut ajouter les probabilités dobtenir 101 cas, puis 102, puis 103, jusquà 500.
P = (X=101) + (X=102) +
..+ (X=500), le calcul est donc inhumain.
Approximation dune loi Binomiale par une loi Normale N (75 ; 7,98)
Là je ne suis pas sûre de moi :
Je pose X* = X-75 > 100 75
7.98 7.98
X* > 3.13 ce nest pas possible, car je ne le retrouve pas dans ma table
Après, je suis coincée, aidez moi si vous pouvez, merci beaucoup.
Est-ce faux si jécris cela :
P (X*> 3.1) = 1- ;) 3.1
= 1 O.99904
= 0.00096
P (X*> 3.2) = 1- ;) 3.2
= 1 O.99931
= 0. 00069
Lapproximation se trouve dans lintervalle :
0.00096 > X* > 0. 00069
Probabilité : loi Binomiale par loi Normale
4 messages
- Page 1 sur 1
bonjour
une remarque tout d'abord je suis choqué qu'un exercice scolaire traite explicitement d'une maladie précise qui tue des millions de personnes ici ou ailleurs;parlerd'un virus oui du virus du sida non.
500>= X>=100 et un encadrement sur X* ensuite les valeurs ne sont peut -être pas dans ta table tabulée souvent jusqu'à 3 et quelques
une remarque tout d'abord je suis choqué qu'un exercice scolaire traite explicitement d'une maladie précise qui tue des millions de personnes ici ou ailleurs;parlerd'un virus oui du virus du sida non.
500>= X>=100 et un encadrement sur X* ensuite les valeurs ne sont peut -être pas dans ta table tabulée souvent jusqu'à 3 et quelques
Salut,
Pour la question 3 je dirais plutôt X* suit une loi normale de paramètres 75 et 7,89. On a alors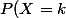\simeq P(k-0.5100)\simeq P(X*>100.5)) .
.
Ensuite on centre et on réduit comme tu l'as fait et on trouve\simeq 1 - \Pi(3.2)\simeq 0,00069) .
.
La fin de ta réponse, elle aussi, est mal écrite :
Ce que tu voulais dire (je crois) est :
ce n'est pas exactement pareil et ça pourrait-être une réponse correcte.
n'a pas de sens (même si on peut deviner ce que tu veux dire)
Pour la question 3 je dirais plutôt X* suit une loi normale de paramètres 75 et 7,89. On a alors
Ensuite on centre et on réduit comme tu l'as fait et on trouve
La fin de ta réponse, elle aussi, est mal écrite :
est un évènement.0.00096 > X* > 0. 00069
Ce que tu voulais dire (je crois) est :
0.00096 > P(X*>100) > 0. 00069
ce n'est pas exactement pareil et ça pourrait-être une réponse correcte.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
