Probabilité et indépendance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 17 Avr 2016, 13:35
par Ncdk » 17 Avr 2016, 13:35
Bonjour,
Soit
)
une suite de variables aléatoires indépendantes et de même loi de Bernouilli
)
avec
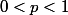
.
Soit

une variable aléatoire discrète à support dans

, indépendante de
)
. On pose :

1) Si
=B(n,\pi))
, montrer que

suit la loi binomiale
)
2) Si
 = P(\lambda))
, montrer que

suit la loi de Poisson
)
.
1) Soit
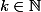
,
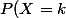=P(\sum_{l=1}^Y Z_l=k)=P(\bigcup_{i=0}^n (\{Y=i\} \cap \{\sum_{l=1}^i Z_l=k\})))
(C'est une union disjointe)
Je comprend pas la dernière égalité, en fait une fois que j'ai cette égalité et que je l'ai compris, le reste c'est du calcul, mais je bloque, je comprend pas ce passage.
Si vous avez une explication, ça serait génial

Modifié en dernier par
Ncdk le 17 Avr 2016, 14:15, modifié 1 fois.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Avr 2016, 14:03
par zygomatique » 17 Avr 2016, 14:03
Ncdk a écrit:Bonjour,
Soit
)
une suite de variables aléatoires indépendantes et de même loi de Bernouilli
)
avec
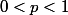
.
Soit

une variable aléatoire discrète à support dans

, indépendante de
)
. On pose :

1) Si
=B(n,\pi))
, montrer que

suit la loi binomiale
)
2) Si
 = P(\lambda))
, montrer que

suit la loi de Poisson
)
.
1) Soit
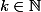
,
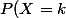=P(\sum_{l=1}^Y Z_l=k)=P(\bigcup_{i=0}^n (\{Y=i\} \cap \{\sum_{l=1}^Y Z_l=k\})))
(C'est une union disjointe)
Je comprend pas la dernière égalité, en fait une fois que j'ai cette égalité et que je l'ai compris, le reste c'est du calcul, mais je bloque, je comprend pas ce passage.
Si vous avez une explication, ça serait génial

salut
ça veut dire quoi : si L(Y) = B(n, pi) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 17 Avr 2016, 14:14
par Ncdk » 17 Avr 2016, 14:14
Ah oui !
J'ai fait une faute déjà, dans mon égalité, la deuxième somme c'est pas Y la borne mais i, j'ai oublié de changer l'indice.
ça signifie : Si la loi de

suit une loi binomiale de paramètre

, ...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Avr 2016, 14:57
par zygomatique » 17 Avr 2016, 14:57
de paramètre pi ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 17 Avr 2016, 15:18
par Ncdk » 17 Avr 2016, 15:18
Oui avec n étapes quoi, enfin la loi binomiale


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Avr 2016, 16:25
par zygomatique » 17 Avr 2016, 16:25
une loi binomiale est définie avec deux paramètres :
le premier est entier et désigne la taille de l'échantillon ou le nombre de répétition de la même expérience de Bernoulli
le deuxième est un réel de l'intervalle [0,1] qui donne la probabilité de succès dans ladite expérience de Bernoulli
il ne me semble pas que pi appartienne à l'intervalle [0, 1] ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Avr 2016, 17:09
par Ben314 » 17 Avr 2016, 17:09
Salut,
Ncdk a écrit:1) Soit
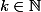
,
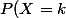=P(\sum_{l=1}^Y Z_l=k)=P(\bigcup_{i=0}^n (\{Y=i\} \cap \{\sum_{l=1}^i Z_l=k\})))
(C'est une union disjointe)
Perso, j'aurais plutôt écrit que :
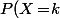=\sum_{i=0}^nP(Y\!=\!i)\!\times\!P\Big(\sum_{\ell=1}^Y Z_\ell=k\,|\, Y\!=\!i\Big)=\sum_{i=0}^nP(Y\!=\!i)\!\times\!P\Big(\sum_{\ell=1}^i Z_\ell=k\Big))
Mais ça revient totalement exactement au même que ton truc (sauf que je trouve ça plus lisible...)
@zygomatique : le

, il joue le même rôle que

, c'est une proba donnée au départ.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 17 Avr 2016, 19:34
par Ncdk » 17 Avr 2016, 19:34
@Zygomatique : En effet,

est juste une notation, qui prend ses valeurs dans

@Ben : Le soucis est que je comprend pas l'histoire avec l'union, pouvoir jongler d'un côté de l'égalité à l'autre, pour moi je ne connais pas la logique, je me pose pas les bonnes questions peut-être.
Je sais pas si on peut l'expliquer par une phrase, je pense que ça me ferait comprendre l'astuce ou la logique du calcul


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 18 Avr 2016, 17:15
par zygomatique » 18 Avr 2016, 17:15
ouais .. j'ai pas tilté ...!!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
une suite de variables aléatoires indépendantes et de même loi de Bernouilli
avec
.
une variable aléatoire discrète à support dans
, indépendante de
. On pose :
, montrer que
suit la loi binomiale
)
, montrer que
suit la loi de Poisson
.
,
(C'est une union disjointe)
,
(C'est une union disjointe)
