j'aurai besoin d'aide pour calculer la somme ;)k/2^(k+1); k allant de 0 à + l'infini
j'avais toruvé que c'etait 1, quelqu'un pourrait me confirmer ce resultat.
la somme en question correspond a l'experance E(X)
X= variable aleatoire a valeurs dans N
et elle suit la loi de probabilité :
pour k dans N, P(X=k)=1/2^(k+1)
Merci d'avance
Probabilite et esperance
4 messages
- Page 1 sur 1
salut,
on pose
Une primitive de S, que jnote Sp est
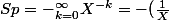^k)
Cette derniere se calcule :

pourvu que , cqui est le cas si X vaut 2.
, cqui est le cas si X vaut 2.
Ici, il me semble qu'il faut parler de convergence uniforme pour dire intervertion des signes integrales et series, mais jmen rappele plus.
On dérive alors Sp pour retrouver S :
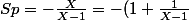 = \frac{1}{1-X} - 1)
D'ou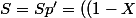^{-1})' = (1-X)^{-2})
Enfin, = 1)
on pose
Une primitive de S, que jnote Sp est
Cette derniere se calcule :
pourvu que
Ici, il me semble qu'il faut parler de convergence uniforme pour dire intervertion des signes integrales et series, mais jmen rappele plus.
On dérive alors Sp pour retrouver S :
D'ou
Enfin,
la vie est une fête 
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
