Salut,
J'ai l'impression qu'au niveau des calculs, dans un cas pareil, c'est plutôt plus simple de prendre comme "pseuso chaine de Markov" celle uniquement constituée des états "Bonus=0", "Bonus=1", ..., "Bonus=16"
sans avoir d'état correspondant à "Fin de l'action".
Ta matrice de transition est alors
_{0\leq i,j\leq 16})
où
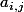
est la proba de passer de l'état "Bonus=j" à l'état "Bonus=i"
et où les proba. de "Fin de l'action" n'apparaissent pas.
Ce n'est donc pas une vraie chaine de Markov vu que la somme des proba par colonne ne fait pas systématiquement 1 (*), mais ça a l'énorme avantage que

est une matrice triangulaire inférieure dont les terme de la diagonale sont <1 donc
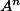
tend vers 0 et ça simplifie (grandement) les différentes preuves (en fait, on est dans un cas extrêmement simple de chaine de Markov dans lequel on ne peut "aller que dans un sens").
Donc, si on note

le vecteur colonne contenant les proba. d'être dans les situation "Bonus=?" après

étapes alors
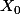
est connu (des 0 partout et un 1 correspondant au bonus de départ) et la "règle" de calcul est évidement
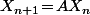
donc
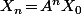
.
La somme des coordonnées de

, c'est à dire
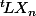
où L est le vecteur colonne formé de 1 correspond alors à la proba de ne pas avoir fini l'action au bout de

étapes.
Donc la proba d'avoir fini au bout de n étapes est
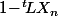
et la proba de finir exactement à la

-ième étape (
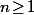
) est
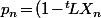\!-\!(1\!-\!^{t}\!LX_{n-1})\!=\!^{t}\!L(A^{n-1}\!-\!A^n)X_0)
.
L'espérance cherchée est donc
X_0\!=\!\lim_{n\to\infty}\null^{t}\!L\Big(\sum_{k=0}^{n}A^{k}\!-\!nA^{n}\Big)X_0)
Or, vu que

est triangulaire avec des valeur sur la diagonale dans [0,1[ la série
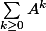
converge vers
^{-1})
(qui existe) et
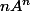
tend vers la matrice nulle et on a en fait le résultat suivant :
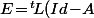^{-1}X_0\!=\!^{t}\!\tilde L X_0)
où
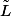
est la solution du système
\tilde L\!=\!L)
.
Bref, le seul calcul qu'il y a à faire, c'est la résolution du système linéaire (et triangulaire !!!)
\tilde L\!=\!L)
qui contient précisément les espérances cherchées (i.e. celle correspondant à un bonus de départ=0, =1, ...)
(*) Par rapport à la "vrai" matrice de transition avec un état de plus "Fin de l'action", on a simplement enlevé la dernière ligne et la dernière colonne.
EDIT : En fait, la formule finale s'explique très simplement :
Si
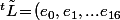)
correspond aux espérance partant d'un bonus de départ égal à 0,1,...,16.
Partant d'un bonus égal à

on a une proba de
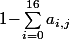
de gagner en un coup et, pour

de 0 à 16 une proba de
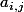
de passer au coup suivant à l'état "Bonus =

" où on gagnera en moyenne en un temps égal à
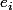
donc, c'est que :
\!\times\!1\!+\!\sum_{i=0}^{16}a_{i,j}\!\times\!(1\!+\!e_i)=1\!+\!\sum_{i=0}^{16}a_{i,j}e_i)
Ce qui, matriciellement parlant, signifie que
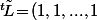\!+\!\null^t\!\tilde LA)
et c'est bien la même chose que le
\tilde L\!=\!L)
trouvé ci dessus.


 Et aussi qu'une moyenne des n se fait avec des coefficients dont la somme vaut 1...
Et aussi qu'une moyenne des n se fait avec des coefficients dont la somme vaut 1...