bonjour, pourriez vous m'aider pour cet exo svp?
je connais la méthode pour prouver la décroissance ou non d'une fonction, mais je n'arrive pas à l'appliquer à cette fonction, ni à trouver sa primitive..
Merci!
Primitive de (tanx) ^n
6 messages
- Page 1 sur 1
Re: primitive de (tanx) ^n
bjr,
question 2: il s'agit de la décroissance d'une suite et non pas de la décroissance d'une fonction
question 3:
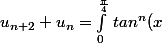 (tan^2(x)+1) dx)
puis poser le changement de variable u=tan(x)
question 2: il s'agit de la décroissance d'une suite et non pas de la décroissance d'une fonction
question 3:
puis poser le changement de variable u=tan(x)
Re: primitive de (tanx) ^n
salut
que peut-on dire de tan x sur l'intervalle [0, pi/4] ?
que peut dire de la suite des fonctions ou termes x^n sur l'intervalle [0, 1] ?
que peut-on dire des intégrales de deux fonctions f et g sur l'intervalle [a, b] sachant que f =< g ?
que peut-on dire de tan x sur l'intervalle [0, pi/4] ?
que peut dire de la suite des fonctions ou termes x^n sur l'intervalle [0, 1] ?
que peut-on dire des intégrales de deux fonctions f et g sur l'intervalle [a, b] sachant que f =< g ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: primitive de (tanx) ^n
mathelot a écrit:bjr,
question 2: il s'agit de la décroissance d'une suite et non pas de la décroissance d'une fonction
question 3:
puis poser le changement de variable u=tan(x)
Bonjour à tous,
Toujours au sujet de la 3) :
On sait que :
On reconnaît donc une forme
Pour la 1) :
Pour la 2) :
Je commence et puis je te laisse terminer en suivant les indications de @Zigomatique :
Pour conclure, il suffit de regarder le signe de
MJoe.
Re: primitive de (tanx) ^n
bobi44 a écrit: je n'arrive pas à l'appliquer à cette fonction, ni à trouver sa primitive..
ce que l'on cherche, c'est plutôt la valeur d'une intégrale (quadrature) qu'une primitive.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
