Bonjours j'aurais besoin de votre aide pour la primitive :
(t-pi)*(- (1/n)cos ;);))
merci de votre aide
Primitive
8 messages
- Page 1 sur 1
euuu je ne c'est pas trop voila je doit effectuer ce DM mais je n'est pas les cours étant nouveau dans l'établissement ( cause de déménagement).
voici le lien du DM :
https://www.dropbox.com/sh/44yd9qqawehgo77/GZDruNhjeu/20140217_134628.jpg
j'aimerais avoir un peut d'explication si une personne de très charitable passe sur mon post
En vous remerciant par avance.
voici le lien du DM :
https://www.dropbox.com/sh/44yd9qqawehgo77/GZDruNhjeu/20140217_134628.jpg
j'aimerais avoir un peut d'explication si une personne de très charitable passe sur mon post
En vous remerciant par avance.
jomath a écrit:euuu je ne c'est pas trop voila je doit effectuer ce DM mais je n'est pas les cours étant nouveau dans l'établissement ( cause de déménagement).
voici le lien du DM :
https://www.dropbox.com/sh/44yd9qqawehgo77/GZDruNhjeu/20140217_134628.jpg
j'aimerais avoir un peut d'explication si une personne de très charitable passe sur mon post
En vous remerciant par avance.
pour ton exercice il s'agit de faire 2 intégrations par parties successives
tu dois donc refaire une intégration par parties pour calculer l'intégrale de 0 à pi de (t-pi)sin(nt)
Bonjour.
@jomath.
On te demande de montrer que si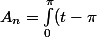^2\cos(nt)dt) et
et 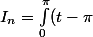\sin(nt)dt) alors
alors  et
et  .
.
 et
et  se présentent toutes deux sous la forme
se présentent toutes deux sous la forme f(t)dt) où
où =\sin(nt)) ou
ou =\cos(nt)) et
et ) un polynôme de degré
un polynôme de degré  . Soit g(t) une primitive de f(t), alors
. Soit g(t) une primitive de f(t), alors
f(t)dt=\left[P_n(t)g(t)\right]_0^{\pi} -\int_0^{\pi}P'_n(t)g(t)dt)
g(t)d) est elle même à un coefficient multiplicatif près de la forme
est elle même à un coefficient multiplicatif près de la forme f(t)dt) puisque
puisque ) est un polynôme de degré
est un polynôme de degré  et
et ) est de forme
est de forme) avec K une constante (
avec K une constante ( ).
).
@jomath.
On te demande de montrer que si
Bonsoir,
j'ai essayé de faire An, mais pas sûr que ce soit bon. (Excusez moi d'avance, je ne sais pas faire les signes d'intégrale avec pi et 0...)
l'intégrale d'An = (t - pi )² cos nt dt
pour u = ( t - pi )² donc u' = 2t -2pi
pour v' = cos nt donc v = 1/n sin nt
Ce qui donne :
An = [ (t - pi)² * 1/n sin nt ] - (2t - 2pi * (1/n sin nt)
------------------------------------------------------------------------------------------------
J'ai donc refait une intégration (celle en gras)
qui donne : (2t - 2pi * (1/n sin nt)
pour u = (2t -2pi) donc u' = 2
pour v' = (1/n sin nt) donc v = -(1/n²) cos nt
[2t - 2pi * (-(1/n²) cos nt)] - ( 2 * ( -(1/n²) cos nt )
Donc si je me trompe pas, ça doit donner :
[2t - 2pi * (-(1/n²) cos nt)] - ( 2t * ( - (1/n³) sin nt) ?
On doit bien refaire la primitive de "( 2 * ( -(1/n²) cos nt )"
= [(2t - 2pi * (-(1/n²) cos nt)] - [ 2t * (-(1/n³) sin nt)
= [ [ (2pi - 2pi * (-(1/n²) cos pin] - [ 2pi * (-(1/n³ sin pin)] ] - [ 2*0 - 2pi * (-(1/n²) cos 0n) - [ 2*0 * (-(1/n³) sin 0n)]
= [ [ 0 * (-(1/n²) cos pin) ] - [ -(2pi/n³) sin pin ] ] - [ 0 - 2pi * (-(1/n²) * 1) - [ 0 * (-(1/n³) * 0 ] ]
= [ 0 - 0 ] - [ (2pi/n²) * 1) ]
= (-(2pi/n²)).
-------------------------------------------------------------------------------------------------
Maintenant faut donc retourner à la première intégration suivante :
An = [ (t - pi)² * 1/n sin nt ] - (2t - 2pi * (1/n sin nt)
Et remplacer : "(2t - 2pi * (1/n sin nt)" par "(-(2pi/n²))" ????
Ce qui donnerai : [ (t - pi)² * 1/n sin nt ] - (- (2pi/n²)) ????
Avec toujours la même intégration entre pi et 0 (encore désolé de pas savoir faire le signe d'intégration)
Ce qui donnerai :
=> [ (t-pi)² * 1/n sin nt ] - (2pi/n) ???? On doit bien refaire la primitive de (- (2pi/n²)) ???
Et donc on est reparti pour un tour :
J'ai essayé en faisant la primitive de "(- (2pi/n²))" et essayé sans pour être sûr.
En faisant la primitive :
[ [ (pi - pi)² * (1/n) sin pin ] - (2pi/n) ] - [ (0-pi)² * 1/0 sin 0n ] - (2pi/n) ]
= [ (0) - (2pi/n) ] - (2pi/n)
donc faux selon l'exo.
Sans faire la primitive :
[ [ (pi - pi)² * (1/n) sin pin ] - (-(2pi/n²)) ] - [ (0-pi)² * 1/0 sin 0n ] - (-(2pi/n²)) ]
= [ 0 + (2pi/n²) ] - (2pi/n²)
= 0
Qui fait que dans mes deux solutions, aucune n'est bonne t.t
Ou alors je me suis planté quelque part mais je ne vois pas où..
J'ai essayé de faire au plus claire, sachant que je n'ai pu mettre les symboles et autres.
Voilou
j'ai essayé de faire An, mais pas sûr que ce soit bon. (Excusez moi d'avance, je ne sais pas faire les signes d'intégrale avec pi et 0...)
l'intégrale d'An = (t - pi )² cos nt dt
pour u = ( t - pi )² donc u' = 2t -2pi
pour v' = cos nt donc v = 1/n sin nt
Ce qui donne :
An = [ (t - pi)² * 1/n sin nt ] - (2t - 2pi * (1/n sin nt)
------------------------------------------------------------------------------------------------
J'ai donc refait une intégration (celle en gras)
qui donne : (2t - 2pi * (1/n sin nt)
pour u = (2t -2pi) donc u' = 2
pour v' = (1/n sin nt) donc v = -(1/n²) cos nt
[2t - 2pi * (-(1/n²) cos nt)] - ( 2 * ( -(1/n²) cos nt )
Donc si je me trompe pas, ça doit donner :
[2t - 2pi * (-(1/n²) cos nt)] - ( 2t * ( - (1/n³) sin nt) ?
On doit bien refaire la primitive de "( 2 * ( -(1/n²) cos nt )"
= [(2t - 2pi * (-(1/n²) cos nt)] - [ 2t * (-(1/n³) sin nt)
= [ [ (2pi - 2pi * (-(1/n²) cos pin] - [ 2pi * (-(1/n³ sin pin)] ] - [ 2*0 - 2pi * (-(1/n²) cos 0n) - [ 2*0 * (-(1/n³) sin 0n)]
= [ [ 0 * (-(1/n²) cos pin) ] - [ -(2pi/n³) sin pin ] ] - [ 0 - 2pi * (-(1/n²) * 1) - [ 0 * (-(1/n³) * 0 ] ]
= [ 0 - 0 ] - [ (2pi/n²) * 1) ]
= (-(2pi/n²)).
-------------------------------------------------------------------------------------------------
Maintenant faut donc retourner à la première intégration suivante :
An = [ (t - pi)² * 1/n sin nt ] - (2t - 2pi * (1/n sin nt)
Et remplacer : "(2t - 2pi * (1/n sin nt)" par "(-(2pi/n²))" ????
Ce qui donnerai : [ (t - pi)² * 1/n sin nt ] - (- (2pi/n²)) ????
Avec toujours la même intégration entre pi et 0 (encore désolé de pas savoir faire le signe d'intégration)
Ce qui donnerai :
=> [ (t-pi)² * 1/n sin nt ] - (2pi/n) ???? On doit bien refaire la primitive de (- (2pi/n²)) ???
Et donc on est reparti pour un tour :
J'ai essayé en faisant la primitive de "(- (2pi/n²))" et essayé sans pour être sûr.
En faisant la primitive :
[ [ (pi - pi)² * (1/n) sin pin ] - (2pi/n) ] - [ (0-pi)² * 1/0 sin 0n ] - (2pi/n) ]
= [ (0) - (2pi/n) ] - (2pi/n)
donc faux selon l'exo.
Sans faire la primitive :
[ [ (pi - pi)² * (1/n) sin pin ] - (-(2pi/n²)) ] - [ (0-pi)² * 1/0 sin 0n ] - (-(2pi/n²)) ]
= [ 0 + (2pi/n²) ] - (2pi/n²)
= 0
Qui fait que dans mes deux solutions, aucune n'est bonne t.t
Ou alors je me suis planté quelque part mais je ne vois pas où..
J'ai essayé de faire au plus claire, sachant que je n'ai pu mettre les symboles et autres.
Voilou
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
