Position asymptote oblique

[Palazz]

Bonjour, j’ai la fonction f(x)=x-3+(3x-5)/(x-2)^2 et je dois étudier la position de l’asymptote Oblique mais je ne sais pas comment m’y prendre.
Merci de bien vouloir m’aider.

[capitaine nuggets]

Salut !

L'asymptote oblique ayant pour équation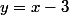 , il faut étudier le signe de .
Elle sera au-dessus si et en-dessous si .

[Palazz]

Oui mais ça reviens à étudier le signe de (3x-5)/(x-2)^2 et je trouve positif au dessus de 5/3 et négatif en dessous mais je ne sais pas comment interpréter ce résultat

Photo du tableau de signe :

[Aispor]

Salut, en parlant d'asymptote ici on ne doit demander que le comportement de la fonction au voisinage de
Donc ce qu'il faudrait juste dire c'est que la courbe de f est au dessus de son asymptote oblique au voisinage de l'infini.

[Aispor]

N'hésite pas en géométrie à vérifier tes résultats sur geogebra (en ligne)

Ici en vert tu as le graphe de ta fonction.
En noir l'asymptote.