Polynômes et racines multiples

par **Nightmare** » 18 Avr 2010, 17:16

Salut :happy3:

Pas très difficile mais amusant :

Soit un polynôme (réel ou complexe, plus généralement en caractéristique nulle).

On note . Montrer que P n'admet aucune racine non nulle d'ordre supérieur à p.

:happy3:

par **girdav** » 18 Avr 2010, 18:31

Bonjour,
si on prend

,

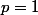
et pour

est plus qu'une simple racine simple.

par **Nightmare** » 18 Avr 2010, 18:35

Salut :happy3:

C'est corrigé : racine non nulle !

par **Doraki** » 18 Avr 2010, 19:03

Je trouve que P n'a pas de racine non nulle d'ordre supérieur ou égal à p.

par **Nightmare** » 18 Avr 2010, 19:07

C'est bien ce qu'il faut montrer !

par **Nightmare** » 19 Avr 2010, 13:47

Pas d'idées?

par **ffpower** » 19 Avr 2010, 14:21

Doraki semble en avoir, mais puisqu'il n'en dit pas plus, je me lance :we:

J'écris P sous la forme

Je suppose que 1 est racine d'ordre au moins p ( on peut facilement se ramener à ce cas là par dilatation ). En écrivant les dérivées successives de P en 1, on obtient:

ect...

C'est un systeme linéaire en a_1...a_p à la Vandermonde.Je veux dire qu'on peux voir qu'il est inversible en se ramenant à un Vandermonde, ou en adaptant la preuve qu'un Vandermonde est inversible, au choix ( ma préférence allant pour la 2eme solution-ca fait moins artificiel ). Bref, au final, on obtient donc que tous les a_k sont nuls, et donc que P est nul ( auquel cas l'exactitude de l'énoncé dépend surtout des conventions que l'on adopte, mais on va dire que P est supposé non nul hein^^ )

par **Nightmare** » 19 Avr 2010, 14:46

Ca me va :happy3:

Polynômes et racines multiples

Polynômes et racines multiples

Qui est en ligne