Bonjour,
Je bloque sur l'exercice suivant :
Déterminer (a, b, c) dans Q pour qu'ils soient racines de X³ + aX² + bX + c
J'en tire trois équations :
2a³ + ba + c = 0
b³ + ab² + ba + c = 0
c³ + ac² + bc + c = 0
On peut factoriser la dernière équation par c, mais la suite me paraît laborieuse.. peut-être que je suis sur la mauvaise piste ?
Merci
Polynômes maths spé
14 messages
- Page 1 sur 1
Re: Polynômes maths spé
Oui, effectivement, j'ai mal recopié mon brouillon, merci !
Mais je bloque toujours autant
Mais je bloque toujours autant
Re: Polynômes maths spé
Bonjour,
Si l'énoncé ne demande pas de trouver toutes les solutions possibles ("déterminer trois rationnels..." mais pas "déterminer tous les triplets de rationnels..."), alors il y a un triplet évident :)
Si l'énoncé ne demande pas de trouver toutes les solutions possibles ("déterminer trois rationnels..." mais pas "déterminer tous les triplets de rationnels..."), alors il y a un triplet évident :
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Polynômes maths spé
hdci a écrit:Bonjour,
Si l'énoncé ne demande pas de trouver toutes les solutions possibles ("déterminer trois rationnels..." mais pas "déterminer tous les triplets de rationnels..."), alors il y a un triplet évident :
Bonjour,
J'ai recopié l'énoncé tel quel, mai je pense que le but de l'exercice se porte plutôt sur la recherche de tous les triplets
Re: Polynômes maths spé
En poursuivant plus loin, si on cherche les solutions possibles avec 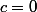 , on peut faire des simplifications et on en tire
, on peut faire des simplifications et on en tire
=0)
=0)
En supposant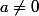 (donc
(donc 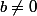 par la première ligne), on aboutit à une équation du second degré en
par la première ligne), on aboutit à une équation du second degré en  qui n'a pas de racines rationnelles...
qui n'a pas de racines rationnelles...
(Correction : OUPS, c'est faux ce que j'ai écrit ici, en fait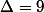 il y a donc des racines rationnelles... Le temps de corriger... Voir plus bas)
il y a donc des racines rationnelles... Le temps de corriger... Voir plus bas)
Donc et en supposant
et en supposant 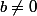 on trouve une unique solution qui est
on trouve une unique solution qui est 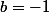
D'où un second triplet est) et
et  est bien solution de
est bien solution de 
En supposant
(Correction : OUPS, c'est faux ce que j'ai écrit ici, en fait
Donc
D'où un second triplet est
Modifié en dernier par hdci le 01 Nov 2019, 11:32, modifié 3 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Polynômes maths spé
ma piste conduisait à des calculs trop compliqués; avec c=0 c'est mieux mais pas simple
Re: Polynômes maths spé
A ce stade j'arrive effectivement à deux solutions, ) et
et ) qui sont les deux seules solutions où
qui sont les deux seules solutions où 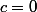
Si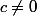 j'ai regardé la piste suggérée par Psigma, mais on arrive à des équations du 3ème degré en
j'ai regardé la piste suggérée par Psigma, mais on arrive à des équations du 3ème degré en  ou en
ou en  , ou à une équation du second degré en
, ou à une équation du second degré en  mais qui est trop affreuse pour être détaillée...
mais qui est trop affreuse pour être détaillée...
Si
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Polynômes maths spé
hdci a écrit:A ce stade j'arrive effectivement à deux solutions,et
qui sont les deux seules solutions où
Sij'ai regardé la piste suggérée par Psigma, mais on arrive à des équations du 3ème degré en
ou en
, ou à une équation du second degré en
mais qui est trop affreuse pour être détaillée...
Merci à vous, la démarche est très claire. Pour le cas c ≠ 0, on pourrait également passer par la dernière ligne de mon système initial, et on arrive à du second degré en c.. mais alors il y a de nouveau une disjonction de cas selon la valeur sur discriminant, et je pense aussi obtenir des expressions assez affruses..
Re: Polynômes maths spé
Après correction de mon erreur (trois ou quatre post plus haut), dans le cas  on obtient d'une part
on obtient d'une part  puis par substitution
puis par substitution

Ce qui donne deux solutions :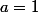 et
et 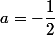
Alors on a respectivement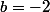 et
et 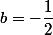
D'où finalement les 4 solutions avec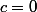
 ; (0,-1,0) ; (1,-2,0) ; \Big(-\dfrac{1}{2},-\dfrac{1}{2},0\Big))
Ce qui donne deux solutions :
Alors on a respectivement
D'où finalement les 4 solutions avec
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Polynômes maths spé
je pige pas votre méthode.
je développe (x-a)(x-b)(x-c)
j'ai le système
-abc=c
ab+bc+ca=b
2a+b+c=0
c=0 me donne (0,0,0) et (1,-2,0) comme solution
c non nul donne
ab=-1
ab+bc+ca=b
2a+b+c=0
je développe (x-a)(x-b)(x-c)
j'ai le système
-abc=c
ab+bc+ca=b
2a+b+c=0
c=0 me donne (0,0,0) et (1,-2,0) comme solution
c non nul donne
ab=-1
ab+bc+ca=b
2a+b+c=0
Re: Polynômes maths spé
pascal16 a écrit:c=0 me donne (0,0,0) et (1,-2,0) comme solution
C'est vrai à condition de considérer que a, b et c sont les seules racines (éventuellement multiples)
Mais on pourrait avoir
Ceci dit, en supposant que
C'est-à-dire (sauf erreur...)
Les deux discriminants doivent être des carrés de rationnels : en particulier celui de la seconde ligne est
Si
si c=-1 la dernière ligne donne
On en tire
Pour terminer, il faudrait montrer que
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Polynômes maths spé
qsdwa a écrit:Bonjour,
Je bloque sur l'exercice suivant :
Déterminer (a, b, c) dans Q pour qu'ils soient racines de X³ + aX² + bX + c
J'en tire trois équations :
2a³ + ba + c = 0
b³ + ab² + ba + c = 0
c³ + ac² + bc + c = 0
On peut factoriser la dernière équation par c, mais la suite me paraît laborieuse.. peut-être que je suis sur la mauvaise piste ?
Merci
Salut,
En employant l'artillerie lourde des bases de Grobner sur SAGE dans l'idéal de l'anneau des polynomes multivariés, j'ai trouvé que c est solution de:
c * (c - 1) * (2*c^2 + c + 1) * (c^3 + 2*c - 1) * (4*c^4 - 4*c^3 + 6*c^2 - 2*c + 1) * (c^8 + 2*c^7 + 6*c^6 + 10*c^5 + 20*c^4 + 12*c^3 + 26*c^2 + 8) = 0
Il suffit donc de voir laquelle des valeurs de c est dans Q pour commencer.
Tout compte fait, les seules solutions rationnelles semblent être:

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
