Bonsoir,
Je rencontre des difficultés pour l'exercice suivant. Cela fait de longues heures que je passe dessus. En soi, l'exercice ne me semble pas très compliqué mais clairement, je bloque au niveau technique.
Voici l'exercice:
Soit a,b,c, les racines complexes du polynôme X^3 + pX^2 + qX + r (r non nul). Calculer a^n +b^n +c^n sachant que n appartient à l'ensemble {2, 3, 4, -1, -2}.
Pas de problème pour n = 2. Je tombe sur p^2 -2q. Par contre, pour n = 3 et n = 4, je bloque.
pour n = 3, je suis parti de (a + b + c)^3 = -p^3.
J'ai développé le terme de gauche. Je tombe sur -p^3 -6r plus une somme assez infâme multiplié par 3. Je pense qu'il y a une factorisation dans cette somme que je ne vois pas. Je n'arrive pas à avancer. -p^3 a l'ai clairement juste mais pour le reste...
Autant vous dire que pour le degré 4, rien que d'y penser, cela m'effraie.
Pouvez-vous m'éclairer ?
A plus.
Polynôme scindé, relations entre coefficients et racines
12 messages
- Page 1 sur 1
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 11 Déc 2020, 18:20
bonsoir,
en attendant de plus amples explications:
https://fr.wikipedia.org/wiki/Formule_d ... _de_Newton
avec (pour le degré 3):
(a+b+c)= a^2b+ab^2+a^2c+ac^2+b^2c+bc^2+3abc)
De plus , on a:
en attendant de plus amples explications:
https://fr.wikipedia.org/wiki/Formule_d ... _de_Newton
avec (pour le degré 3):
De plus , on a:
Modifié en dernier par mathelot le 11 Déc 2020, 18:40, modifié 1 fois.
Re: Polynôme scindé, relations entre coefficients et racines
par thoralf8weblen » 11 Déc 2020, 18:36
Je suis bien d'accord ! Je tombe sur a^3 + b^3 + c^3 + 3((a^2b) + (a^2)c + (b^2)c + a(b^2) + a(c^2)+ b(c^2)) + 6abc = -p^3 en développant (a + b + c)^3 mais c'est justement à cette étape que je n'arrive pas à progresser. Je n'arrive pas à exploiter cette somme (a^2b) + (a^2)c + (b^2)c + a(b^2) + a(c^2)+ b(c^2)...
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 11 Déc 2020, 18:41
je viens de répondre à ta question (dans mon avant-dernier post)
Re: Polynôme scindé, relations entre coefficients et racines
par thoralf8weblen » 11 Déc 2020, 19:09
Je te remercie vivement !
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 12 Déc 2020, 19:46
Les sommes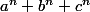 
se calcule par récurrence, en effet pour calculer
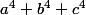il faut connaitre
,
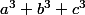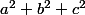et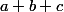 
.
degré 2
^2 = a^2+b^2+c^2 + 2 (ab+ac+bc))
soit
degré 3
regardons les triplets d'exposants, leur somme doit valoir 3:
,(0,3,0),(0,0,3))
soit 
, (2,0,1),(0,2,1))
soit 
,(1,0,2),(0,1,2)
) soit 
)
soit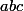 
La formule du multinôme de Newton donne pour le cas n=3:
^3=\dfrac{3!}{3!0!0!} (a^3+b^3+c^3)+\dfrac{3!}{2!1!0!}(a^2b+a^2c+b^2c+ab^2+ac^2+bc^2)+\dfrac{3!}{1!1!1!}abc)
^3=a^3+b^3+c^3+3(a^2b+a^2c+b^2c+ab^2+ac^2+bc^2)+6abc)
or,
(a^2+b^2+c^2)=a^3 +a^2b+a^2c+ab^2+b^3+b^2c+ac^2+bc^2+c^3)
-(a^3+b^3+c^3))+6\sigma_3)
+3(\sigma_1(\sigma_1^2-2\sigma_2)+6\sigma_3)
=3\sigma_1(\sigma_1^2-2\sigma_2)+6\sigma_3-\sigma_1^3)
=2\sigma_1^3-6 \sigma_1\sigma_2+6\sigma_3)
vérifié par notre ami wolfram alpha: https://www.wolframalpha.com/input/?i=% ... %29%2B3abc
degré 2
soit
degré 3
regardons les triplets d'exposants, leur somme doit valoir 3:
La formule du multinôme de Newton donne pour le cas n=3:
or,
vérifié par notre ami wolfram alpha: https://www.wolframalpha.com/input/?i=% ... %29%2B3abc
Modifié en dernier par mathelot le 14 Déc 2020, 14:14, modifié 2 fois.
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 12 Déc 2020, 21:49
degré 4
la formule du multinôme (de Newton) de degré 4 donne:
^4=a^4+b^4+c^4+\dfrac{4!}{3!1!0!}(a^3b+b^3c+ac^3+ab^3+bc^3+a^3c)+\dfrac{4!}{2!2!0!}(a^2b^2+a^2c^2+b^2c^2)+\dfrac{4!}{2!1!1!}(a^2bc+ab^2c+abc^2))
^4=a^4+b^4+c^4+4(a^3b+b^3c+ac^3+ab^3+bc^3+a^3c)+6(a^2b^2+a^2c^2+b^2c^2)+12(a^2bc+ab^2c+abc^2))
or,
(a+b+c)=a^4+ab^3+ac^3+a^3b+b^4+bc^3+a^3c+b^3c+c^4)
d'où:
\sigma_1-(a^4+b^4+c^4=ab^3+ac^3+a^3b+bc^3+a^3c+b^3c)
\sigma_1-(a^4+b^4+c^4))
or,
^2=a^2b^2+a^2c^2+b^2c^2+2(a^2bc+ab^2c+abc^2))
soit
+12(a^2bc+ab^2c+abc^2))
\sigma_1-(a^4+b^4+c^4))+6\sigma_2^2)
=\sigma_1^4-4(\sigma_1^4-3\sigma_1^2\sigma_2+3\sigma_1\sigma_3)-6\sigma_2^2)
=-3\sigma_1^4+12\sigma_1^2\sigma_2-12\sigma_1\sigma_3-6\sigma_2^2)
résultat vérifié par wolfram-alpha:
https://www.wolframalpha.com/input/?i=% ... Bbc%29%5E2
la formule du multinôme (de Newton) de degré 4 donne:
or,
d'où:
or,
soit
résultat vérifié par wolfram-alpha:
https://www.wolframalpha.com/input/?i=% ... Bbc%29%5E2
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 12 Déc 2020, 22:56
degré -1
degré -2
^2}=\dfrac{\sigma_2^2-2\sigma_1\sigma_3}{\sigma_3^2})
degré -2
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 14 Déc 2020, 17:51
pour terminer le taf:
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 14 Déc 2020, 22:37
degré 5
On a des égalités récursives où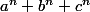 s'exprime avec 
:
(a+b+c)= a^5+b^5+c^5 +(ab^4+ac^4+a^4b+bc^4+a^4c+b^4c))
(a^3+b^3+c^3)=(a^4b+a^4c+ab^4+b^4c+ac^4+bc^4)+(a^3bc+ab^3c+abc^3))
)
^2-2(ab+ac+bc))
on va remonter les quatre dernières lignes:
=\sigma_1^2\sigma_3-2\sigma_2\sigma_3)
-\sigma_1^2\sigma_3+2\sigma_2\sigma_3=a^4b+a^4c+ab^4+b^4c+ac^4+bc^4)
On a des égalités récursives où
on va remonter les quatre dernières lignes:
Modifié en dernier par mathelot le 15 Déc 2020, 12:31, modifié 9 fois.
Re: Polynôme scindé, relations entre coefficients et racines
par GaBuZoMeu » 14 Déc 2020, 22:43
Bonsoir,
Sommes de Newton et identité de Newton : https://fr.wikipedia.org/wiki/Identit%C3%A9s_de_Newton
Sommes de Newton et identité de Newton : https://fr.wikipedia.org/wiki/Identit%C3%A9s_de_Newton
Re: Polynôme scindé, relations entre coefficients et racines
par mathelot » 14 Déc 2020, 23:36
Merci.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :