Points extrêmes !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Aoû 2007, 15:29
par barbu23 » 01 Aoû 2007, 15:29
Bonjour:
Soit :
 \hspace{5cm} : \hspace{5cm} x_{1}^{2}+x_{2}^{2} \leq 1 \hspace{5cm} \} $)
.

est un ensemble convexe de

.
Je cherche à déterminer l'ensemble des points extrêmes de

selon la définition suivante :
 Définition:
Définition:Soit

un convexe de

.
Un point

est un point extrême de

si :
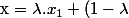.x_{2} $)
avec :
 \in S \times S $)
et

alors :

.

Dans le cours, l'ensemble des points extrêmes de

est
 \hspace{5cm} : \hspace{5cm}x_{1}^{2}+x_{2}^{2} = 1 \hspace{5cm} \} $)
, mais malheureusement, sans démonstration .. !
Merçi d'avance !!
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 01 Aoû 2007, 15:41
par quinto » 01 Aoû 2007, 15:41
Bonjour,
il est clair que si tu prends 2 points sur le cercle, disons x et y, alors toute combinaison convexe de ces points sera dans le disque ouvert.
Ce qui démontre le résultat.
a+
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Aoû 2007, 16:04
par barbu23 » 01 Aoû 2007, 16:04
Oui c'est vrai "quinto" ..., mais je ne vois pas comment utiliser la définition pour arriver au résultat !!
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 01 Aoû 2007, 16:34
par quinto » 01 Aoû 2007, 16:34
Salut,
ête un point extreme w signifie que dès que tu es une combinaisons convexe de x et y alors nécessairement x=y=w.
Si tu prends la contraposée, les points non extrêmes sont ceux qui sont des combinaisons convexes de points distincts. Donc les points extrêmes sont ceux qui ne sont pas des combinaisons convexes de points distincts.
Est-ce clair ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités