Points critiques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
clara69
- Messages: 8
- Enregistré le: 17 Mar 2015, 20:47
-
 par clara69 » 26 Mar 2015, 11:35
par clara69 » 26 Mar 2015, 11:35
Bonjour,
J'ai un problème sur le calcul de points critiques
J'ai
=log(1+x^2y^2))
donc je calcule:

J'obtiens

Donc

=0)
Donc pour les points critiques
(0,b) (a,0) (a,a) avec a,b
???

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Mar 2015, 11:48
par fatal_error » 26 Mar 2015, 11:48
hello,
tu as

qui correspond à deux equations (faut lire un système):

si tu fais l'égalité tu perds une info donc il faut que tu gardes en tete :

De fait
: xy(y-x)=0 \\<br />(2): 2xy^2=0)
donc de (2), x = 0 ou y = 0
si x = 0 c'est solution de (1) donc ok
si y = 0 c'est solution de (1) aussi donc ok
donc tes solutions sont de la forme
(0,a) ou (a,0), a dans R
la vie est une fête

-
clara69
- Messages: 8
- Enregistré le: 17 Mar 2015, 20:47
-
 par clara69 » 26 Mar 2015, 12:12
par clara69 » 26 Mar 2015, 12:12
fatal_error a écrit:hello,
tu as

qui correspond à deux equations (faut lire un système):

si tu fais l'égalité tu perds une info donc il faut que tu gardes en tete :

De fait
: xy(y-x)=0 \\<br />(2): 2xy^2=0)
donc de (2), x = 0 ou y = 0
si x = 0 c'est solution de (1) donc ok
si y = 0 c'est solution de (1) aussi donc ok
donc tes solutions sont de la forme
(0,a) ou (a,0), a dans R
Ok, super merci. Effectivement mon point (a,a) n'est pas un point critique avec le fait que

Donc, j'ai 2 points critiques de la forme (0,a) et (a,0).
En calculant ma hessienne, j'obtiens rt-s²=0 donc pour conclure sur la nature de mes points je dois étudier le signe de
-f(a,0))
et
-f(0,a))
c'est bien çà?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Mar 2015, 12:16
par fatal_error » 26 Mar 2015, 12:16
c'est plus précis que x et y quelconques.
tu veux regarder au voisinage de (a,0) si t'as un mini (local), un maxi(local) ou un point selle.
le plus simple c'est de regarder les valeurs propres de ta hessienne évaluée au point (a,0) par exemple.
pour voir si dans toutes les directions tu vas croitre ou décroitre ou...ca dépend.
la vie est une fête

-
clara69
- Messages: 8
- Enregistré le: 17 Mar 2015, 20:47
-
 par clara69 » 26 Mar 2015, 12:29
par clara69 » 26 Mar 2015, 12:29
fatal_error a écrit:c'est plus précis que x et y quelconques.
tu veux regarder au voisinage de (a,0) si t'as un mini (local), un maxi(local) ou un point selle.
le plus simple c'est de regarder les valeurs propres de ta hessienne évaluée au point (a,0) par exemple.
pour voir si dans toutes les directions tu vas croitre ou décroitre ou...ca dépend.
Sauf erreur de ma part les valeurs propres de ma hessienne (pour (a,0)) sont 0 et
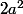
Donc mes valeurs propres sont positives ou nulles donc (a,0) est un minimum local, c'est bien çà?
-
clara69
- Messages: 8
- Enregistré le: 17 Mar 2015, 20:47
-
 par clara69 » 26 Mar 2015, 13:09
par clara69 » 26 Mar 2015, 13:09
En fait le déterminant de ma hessienne est nul pour mes 2 points (a,o) et (0,a).
Donc se sont des points critiques dégénérés non?
Et donc je ne peux rien dire de plus?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Mar 2015, 17:38
par zygomatique » 26 Mar 2015, 17:38
ça veut dire qu'il faut aller à l'ordre 3 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités