Points critiques
26 messages
- Page 2 sur 2 - 1, 2
Pour les deux autres points critiques, c'est O.K.
Pour le "cas général" (en dimension quelconque), le résultat vient du "développement limité" de la fonction f au voisinage d'un point qui s'écrit avec les dérivées partielles (formule de Taylors) :
Si on prend un point de coordonnées (x1+h1,x2+h2,...xn+hn) assez proche du "point de base" (x1,x2,...xn) alors f(x1+h1,x2+h2,...xn+hn) est trés proche de :
f(x1,x2,...xn)
plus la somme de tout les df/dxi(x1,...xn) fois hi
plus la somme de tout les d²f/dxidxj(x1,...xn) fois hi fois hj
Pour avoir un min/max local, il faut que la somme des deux sommes reste de signe constant (lorsque les hi sont proche de 0)
Comme une fonction h->ah ne peut rester de signe constant que lorsque a=0, on trouve comme première condition que les df/dxi douvent tous être nuls.
Pour la deuxième somme, c'est une "forme quadratique" et on essaye de l'écrire comme une somme de carrés pour voir si elle change de signe ou pas. La méthode pour le faire consiste à "faire apparaitre des identités remarquables" (plus une astuce dans un cas particulier)
Par exemple, pour ton point critique (1,-1), la forme quadratique est (en appelant X et Y ce qui au dessus s'apelle h1 et h2) :
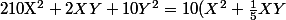+10Y^2=10(X^2+2X\frac{1}{10}Y+(\frac{1}{10}Y)^2-(\frac{1}{10}Y)^2)+10Y^2)
^2-\frac{1}{100}Y^2)+10Y^2<br />=10(X+\frac{1}{10}Y)^2+\frac{99}{10}Y^2\ \geq\ 0)
Donc, les points proche de (-1,1) ont une image plus grande que celle de (-1,1) ce qui signifie que (-1,1) est un minimum local.
Pour le "cas général" (en dimension quelconque), le résultat vient du "développement limité" de la fonction f au voisinage d'un point qui s'écrit avec les dérivées partielles (formule de Taylors) :
Si on prend un point de coordonnées (x1+h1,x2+h2,...xn+hn) assez proche du "point de base" (x1,x2,...xn) alors f(x1+h1,x2+h2,...xn+hn) est trés proche de :
f(x1,x2,...xn)
plus la somme de tout les df/dxi(x1,...xn) fois hi
plus la somme de tout les d²f/dxidxj(x1,...xn) fois hi fois hj
Pour avoir un min/max local, il faut que la somme des deux sommes reste de signe constant (lorsque les hi sont proche de 0)
Comme une fonction h->ah ne peut rester de signe constant que lorsque a=0, on trouve comme première condition que les df/dxi douvent tous être nuls.
Pour la deuxième somme, c'est une "forme quadratique" et on essaye de l'écrire comme une somme de carrés pour voir si elle change de signe ou pas. La méthode pour le faire consiste à "faire apparaitre des identités remarquables" (plus une astuce dans un cas particulier)
Par exemple, pour ton point critique (1,-1), la forme quadratique est (en appelant X et Y ce qui au dessus s'apelle h1 et h2) :
Donc, les points proche de (-1,1) ont une image plus grande que celle de (-1,1) ce qui signifie que (-1,1) est un minimum local.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si, tu as parfaitement raison (mea coulpa..., vraiment désolé)
[Le 2 vient du fait que dans la "formule théorique", le coeff apparait 2 fois : une fois sous la forme d²f/dxdx et une fois sous la forme d²f/dydx]
Cela change pas mal les valeurs numériques dans le calculs, mais ca ne change pas la "philosophie" du calcul...
+10Y^2=10(X^2+2X\frac{1}{5}Y+(\frac{1}{5}Y)^2-(\frac{1}{5}Y)^2)+10Y^2)
^2-\frac{1}{25}Y^2\big)+10Y^2<br />=10(X+\frac{1}{5}Y)^2+\frac{48}{5}Y^2\ \geq\ 0)
En espérant ne pas m'être (re)gourré...
[Le 2 vient du fait que dans la "formule théorique", le coeff apparait 2 fois : une fois sous la forme d²f/dxdx et une fois sous la forme d²f/dydx]
Cela change pas mal les valeurs numériques dans le calculs, mais ca ne change pas la "philosophie" du calcul...
En espérant ne pas m'être (re)gourré...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'ai pas tout compris de ton post...pizzouille a écrit:une dernière question
(1,2) Q(X,Y)=6X²+2*12XY+6Y²
Q(X,Y)=6* ( (x+2Y)² - 3Y²) (dans le cours en exemple)
c'est écrit f ni maximum local ni minimum local
delta > 0
j'ai trouvé mon erreur si c'est bon bien sur
Q(X,Y)=6* ( (x+2Y)² - 3Y²) > 0??
Mais, lorsque l'on écrit la forme quadratique comme une somme de carrés, pour qu'elle reste de signe constant, il faut que tout les coeff devant les carrés soient de même signe (tous positifs => la fonction augmente au alentour du point => c'est un mini local /// tous négatifs => la fonction diminue au alentour du point => c'est un max local)
Lorsque l'on est en dim 2 (et uniquement dans ce cas là), on a :
Delta les deux coeff devant les carrés seront de même signe.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
26 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
