Point de branchement et continuation analytique
14 messages
- Page 1 sur 1
Point de branchement et continuation analytique
Bonjour,
Je viens à vous afin d'être éclairée sur les points de branchement et la continuation analytique. Je suis clairement perdue de comment les déterminer, les trouver.
Par exemple, une de mes questions est : Explorer le comportement en z = z0 et préciser le type de point singulier s'il y en a de f(z)= (2z +3)/(1 + z + 2z^{1/2}), z0 = 1.
Une autre d'entre elles est :
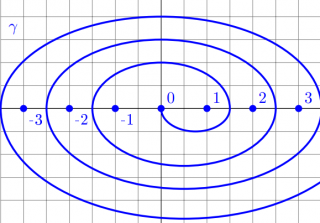
Pour la courbe donnée γ on fixe la branche régulière dans le domaine C \ γ de f (z) = ln z par f (1) = 0. Pour cette branche, trouvez la valeur de sa continuation analytique f (−3) =?
PS : Je suis étudiante dans une université étrangère, mes cours sont donc en anglais. Par conséquent je ne sais pas si mes traductions sont parfaites. Dans mon cours on parle de : "Branch point" et " analytic continuation"
Je viens à vous afin d'être éclairée sur les points de branchement et la continuation analytique. Je suis clairement perdue de comment les déterminer, les trouver.
Par exemple, une de mes questions est : Explorer le comportement en z = z0 et préciser le type de point singulier s'il y en a de f(z)= (2z +3)/(1 + z + 2z^{1/2}), z0 = 1.
Une autre d'entre elles est :
Pour la courbe donnée γ on fixe la branche régulière dans le domaine C \ γ de f (z) = ln z par f (1) = 0. Pour cette branche, trouvez la valeur de sa continuation analytique f (−3) =?
PS : Je suis étudiante dans une université étrangère, mes cours sont donc en anglais. Par conséquent je ne sais pas si mes traductions sont parfaites. Dans mon cours on parle de : "Branch point" et " analytic continuation"
Re: Point de branchement et continuation analytique
Bonjour,
On perle aussi de points de ramification et de prolongement analytique.
Ta première question est un peu bizarre. Ta fonction a deux branches, avec point de ramification en l'origine. Une des branches a un pôle en 1, l'autre y vaut 5/4.
a deux branches, avec point de ramification en l'origine. Une des branches a un pôle en 1, l'autre y vaut 5/4.
Quant à la deuxième question, tu as oublié de dire qui est .
.
On perle aussi de points de ramification et de prolongement analytique.
Ta première question est un peu bizarre. Ta fonction
Quant à la deuxième question, tu as oublié de dire qui est
Re: Point de branchement et continuation analytique
Ma courbe est un spirale partant de zéro en 1 elle vaut -0.5 en 1,5 elle vaut 0, puis elle repasse en zero elle vaut 1, en -1.5 elle vaut 0, en 0 elle vaut -1.5 en 2.5 0 etc, elle ne passe pas par -3 directement. (PS : je ne sais pas si c'est possible de joindre un photo, j'ai essayé mais j'y arrive pas désolée)
Re: Point de branchement et continuation analytique
Je ne m'y retrouve pas avec ta description. Tu peux joindre une image. Le mode d'emploi est ici
https://www.maths-forum.com/guide-utilisation-f41/comment-inserer-une-image-t215647.html#p1404661 :
https://www.maths-forum.com/guide-utilisation-f41/comment-inserer-une-image-t215647.html#p1404661 :
Re: Point de branchement et continuation analytique
<a href='https://www.casimages.com/i/210423120745866481.png.html' target='_blank' title='Mon image'><img src='https://nsa40.casimages.com/img/2021/04/23/210423120745866481.png' border='0' alt='Mon image' /></a>
Je crois que c'est ça
Je crois que c'est ça
Re: Point de branchement et continuation analytique
Ou celui ci après essaye fonctionne bien : https://www.casimages.com/i/210423120745866481.png.html
Re: Point de branchement et continuation analytique
On part de la détermination de la racine carrée fixée par =1) dans le complémentaire de la courbe bleue. En suivant par prolongement, quelle détermination de la racine carrée a-t-on pour -1, 2, -2, 3, -3 ?
dans le complémentaire de la courbe bleue. En suivant par prolongement, quelle détermination de la racine carrée a-t-on pour -1, 2, -2, 3, -3 ?
Re: Point de branchement et continuation analytique
Désolée je ne suis pas très à l'aise avec l'informatique. Cependant maintenant avez vous une idée de comment proceder vis à vis de ma question ?
Re: Point de branchement et continuation analytique
Par ailleurs pour la ma première question je vois pourquoi 1 est une point singulier mais pas 5/4. En effet j'ai procédé comme suit :
Tout d'abord nous pouvons voir que les seul points de branchement de ma fonction sont 0 et l'infini. 1 n'est donc pas un point de branchement il existe donc deux branche en ce point. On pose la première branche : \sqrt{1} = 1 et le deuxième : sqrt{1} = -1. Maintenant on pose w = z - 1, on a donc :
-f(z) = f(w + 1) = (2w+5)/(2 + w - 2\sqrt{w+1}) pour la branche deux. Nous pouvons facilement voir qu'il y a un point singulier : w = 0, donc z = 1, donc 1 est un point singulier, de plus lim(z ->1) f(z) = infini donc 1 est un pole.
- f(z) = f(w+1) = (2w+5)/(2 + w + 2\sqrt{w+1}) pour la première branche, elle n'a pas de point singulier comme nous pouvons le voir car le dénominateur ne s'annule jamais.
Tout d'abord nous pouvons voir que les seul points de branchement de ma fonction sont 0 et l'infini. 1 n'est donc pas un point de branchement il existe donc deux branche en ce point. On pose la première branche : \sqrt{1} = 1 et le deuxième : sqrt{1} = -1. Maintenant on pose w = z - 1, on a donc :
-f(z) = f(w + 1) = (2w+5)/(2 + w - 2\sqrt{w+1}) pour la branche deux. Nous pouvons facilement voir qu'il y a un point singulier : w = 0, donc z = 1, donc 1 est un point singulier, de plus lim(z ->1) f(z) = infini donc 1 est un pole.
- f(z) = f(w+1) = (2w+5)/(2 + w + 2\sqrt{w+1}) pour la première branche, elle n'a pas de point singulier comme nous pouvons le voir car le dénominateur ne s'annule jamais.
Re: Point de branchement et continuation analytique
GaBuZoMeu a écrit:On part de la détermination de la racine carrée fixée pardans le complémentaire de la courbe bleue. En suivant par prolongement, quelle détermination de la racine carrée a-t-on pour -1, 2, -2, 3, -3 ?
On ne pose pas plutôt : ln(z) = ln|z| + iarg(z), et on s'intéresse à la valeur de son argument ? Tout en sachant donc que ln(1) = 0. Par rapport à la courbe j'aurais donc dit que en ln(-1) = ln(1) - i \pi, ln(-2) = ln2 -2\pi ? (mais clairement pas sur j'essaye d'utiliser ce que j'ai vu dans mes cours mais que je suis pas sur d'avoir comprise)
Re: Point de branchement et continuation analytique
1°) Vrai, tu ne vois pas pourquoi la deuxième branche prend la valeur 5/4 en 1 ??? Regarde mieux !
2°) Ce qui nous intéresse ici est la fonction "racine carrée" ; la détermination de cette fonction change de signe quand on fait un tour autour de l'origine.
2°) Ce qui nous intéresse ici est la fonction "racine carrée" ; la détermination de cette fonction change de signe quand on fait un tour autour de l'origine.
Re: Point de branchement et continuation analytique
GaBuZoMeu a écrit:1°) Vrai, tu ne vois pas pourquoi la deuxième branche prend la valeur 5/4 en 1 ??? Regarde mieux !
2°) Ce qui nous intéresse ici est la fonction "racine carrée" ; la détermination de cette fonction change de signe quand on fait un tour autour de l'origine.
1) Je suis d'accord qu'en 1 la deuxième branche prend la valeur 5/4, mais ce n'est pas un point singulier pour autant ?
2) je crois avoir compris cette question merci
Re: Point de branchement et continuation analytique
Azenora a écrit:1) Je suis d'accord qu'en 1 la deuxième branche prend la valeur 5/4, mais ce n'est pas un point singulier pour autant ?
Qui t'a dit que c'était un point singulier pour la deuxième branche ??? Tu lis de travers.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :