Bonjour
Je dois montrer que le rang de Aa est égal à 3 pour tout a ∈ R / {−1/2}:
Aa=
(a+1) 0 a
(-a) 1 -a
a 0 (a+1)
J'aimerai échelonner la matrice en arrivant à une dernière ligne 0 0 2a+1 mais je n'y parviens pas, sauf si je manipule d'abord les colonnes de la matrice avant d'en échelonner les lignes cependant je ne sais pas si j'ai le droit. Ma question est donc la suivante : puis-je faire du pivot de Gauss d'abord sur les colonnes puis ensuite sur les lignes d'une matrice, si non, comment répondre à la question ? Merci de votre aide
Pivot de gauss matrices
7 messages
- Page 1 sur 1
Re: Pivot de gauss matrices
1. Oui tu peux faire autant de manipulations que tu veux sur les lignes et/ou les colonnes.
2. As-tu envisagé une autre piste , qui pourrait être beaucoup plus rapide ?
Qu'est ce qui caractérise une matrice 3x3, de rang 3 ?
2. As-tu envisagé une autre piste , qui pourrait être beaucoup plus rapide ?
Qu'est ce qui caractérise une matrice 3x3, de rang 3 ?
Re: Pivot de gauss matrices
lyceen95 a écrit:1. Oui tu peux faire autant de manipulations que tu veux sur les lignes et/ou les colonnes.
2. As-tu envisagé une autre piste , qui pourrait être beaucoup plus rapide ?
Qu'est ce qui caractérise une matrice 3x3, de rang 3 ?
D'accord merci beaucoup, je n'ai pas eu d'autres pistes pour le moment.
Elle est inversible ?
Re: Pivot de gauss matrices
Oui, une matrice nxn est de rang n, ssi elle est inversible.
Et comment caractérise-t-on une matrice inversible, sans lancer toute la mécanique de calculer son inverse ?
J'espère que le cours que j'ai appris quand j'étais étudiant (tu n'étais pas né) est encore enseigné !
Et comment caractérise-t-on une matrice inversible, sans lancer toute la mécanique de calculer son inverse ?
J'espère que le cours que j'ai appris quand j'étais étudiant (tu n'étais pas né) est encore enseigné !
Re: Pivot de gauss matrices
lyceen95 a écrit:Oui, une matrice nxn est de rang n, ssi elle est inversible.
Et comment caractérise-t-on une matrice inversible, sans lancer toute la mécanique de calculer son inverse ?
J'espère que le cours que j'ai appris quand j'étais étudiant (tu n'étais pas né) est encore enseigné !
je pense que votre cours est toujours d'actualité mais j'avoue que je ne sais pas ... Peut-etre le fait que la famille formée par les colonnes est libre ?
Re: Pivot de gauss matrices
La propriété que j'avais en mémoire est toujours vraie (je n'étais pas inquiet là dessus), mais est-elle toujours enseignée : Une matrice carrée est inversible ssi son déterminant est non nul.
Le point suivant, c'est : sait on calculer le déterminant d'une matrice 3x3.
Ici, le déterminant est assez facile à calculer, grâce aux valeurs 0 :
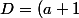^2 -a^2)
Et l'équation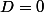 est facile à résoudre.
est facile à résoudre.
Le point suivant, c'est : sait on calculer le déterminant d'une matrice 3x3.
Ici, le déterminant est assez facile à calculer, grâce aux valeurs 0 :
Et l'équation
Re: Pivot de gauss matrices
Bonsoir,
Les opérations élémentaires sur les lignes marchent très bien, par exemple en commençant pas soustraire la 3e ligne de la 1e.
Pas besoin de faire appel au déterminant.
Les opérations élémentaires sur les lignes marchent très bien, par exemple en commençant pas soustraire la 3e ligne de la 1e.
Pas besoin de faire appel au déterminant.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
