Bonjour à toutes et à tous.
J'ai un petit problème sur mon DM.
Je poste le message que j'ai créé sur le forum Ilemaths, ça revient au même que de CC tout le message avec toutes les modifs sur celui-ci que cela impliquerait.
http://www.ilemaths.net/forum-sujet-637087.html#msg5396233
Merci d'avance.
Petit problème algèbre linéaire.
3 messages
- Page 1 sur 1
cours
prop
soit f un endomorphisme de
les propriétés suivantes sont équivalentes:
i) f est surjective
ii) f est injective
iii) f est bijective
Pour trouver un vecteur propre (donc nécessairement non nul)
on cherche les réels tel que
tel que
 non injective
non injective
prop
f de matrice M dans la base canonique
i) non injective
non injective
ii) il existe ,non nul,tel que
,non nul,tel que =\lambda \vec{u})
iii) det=0)
Soit la matrice A de la symétrie s dans la base canonique:

montrer que la recherche de vecteurs propres conduit à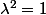
prop
soit f un endomorphisme de
les propriétés suivantes sont équivalentes:
i) f est surjective
ii) f est injective
iii) f est bijective
Pour trouver un vecteur propre (donc nécessairement non nul)
on cherche les réels
prop
f de matrice M dans la base canonique
i)
ii) il existe
iii) det
Soit la matrice A de la symétrie s dans la base canonique:
montrer que la recherche de vecteurs propres conduit à
Pour les valeur propres tu résous:
même chose pour -1.
Pour l'instant, puisque
est
Si tu prends une base de vecteur propre
(à vérifier!) ta matrice va devenir:
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
