Bonjour,
Le dual d'un e.v E est l'ensemble des applications linéaires de E dans le corps des scalaires de E.
Soit f une telle application et x un vecteur quelconque de coordonnées
_{i \in I})
dans la base
_{i \in I})
.
Comme f est linéaire:
=f(\sum_{i \in I} \quad x_{i} e_{i})=\sum_{i \in I} \quad x_{i} f(e_{i})= \sum_{i \in I} \quad f(e_{i})x_{i})
En notant
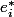
la forme linéaire:
la formule ci-dessus montre que:
Il s'agit d'une combinaison linéaire entre formes si l'ensemble d'indices I
est fini.
Dans ce cas, la famille
)
est donc une famille génératrice de l'espace dual.
C'est tout simplement l'ensemble des coordonnées d'un vecteur, chaque coordonnée étant vue comme une application linéaire.
De plus ,
=\delta_{i,j})
où
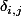
est le symbole de Kronecker.
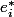
est une famille libre. En effet,
entraine, en testant sur un vecteur de base
.
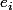
=0=\lambda_{i})
La famille est donc libre. E et son dual sont deux e.v de même dimension
si E est de dimension finie,
mais l'isomorphisme n'est pas canonique. Il dépend du choix d'une base.
Le dual E' possède à son tour un dual, le bidual et cette fois, tjrs en dimension
finie, on a un isomorphisme canonique donné par le crochet de
dualité:
)
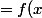qui exprime que l'image f(x) dépend bilinéairement des
deux opérandes.
Dans le cas général,on distingue trois ensembles:
- le dual algébrique, démesuré et pathologique
- le dual topologique, plus raisonnable, formé des formes linéaires continues
- les espaces de Hilbert où l'on considère seulement l'adhérence
de l'e.v engendré par une famille dénombrable d'éléments.
, et je ne parviens donc pas du tout a résoudre cette exercice... :mur: Si quelqu'un pouvait me donner une piste car je plante dès la première question ! D'avance merci beaucoup !