Permanent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 01 Nov 2017, 23:48
par mehdi-128 » 01 Nov 2017, 23:48
Bonsoir,
||.|| désigne la norme euclidienne de

Pour
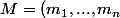 \in M_{n,n} (R))
on définit son permanent de
)^n)
dans

par :
=\sum_{\sigma \in \mathfrak{S}_n}m_{1 \sigma(1)} \times ... \times m_{n \sigma(n)})
1/ Montrer que le permanent d'une matrice M est égale à celui de sa transposée.
Je vois pas trop comment procéder.
2/ Pour
)
et
)
éléments de
)^n)
établir l'inégalité suivante :
-per(r_1,...,r_n)| \leq n! \sum_{j=1}^{n} ||m_1|| ...||m_{j-1}|| \times ||m_j -r_j|| \times ||r_{j+1}||...||r_n||)
Où l'on convient que :
Pour
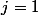
:

et pour
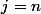

Pas trop compris la dernière ligne et j'ai pas d'idées pour la résolution de la question.
Merci d'avance.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Nov 2017, 00:32
par infernaleur » 02 Nov 2017, 00:32
Salut la formule que tu as écrite pour le permanent me fait penser à celle du déterminant
Donc sa me fait penser a la démonstration que le déterminant d'une matrice est égale au déterminant de la transposée de cette matrice (si tu l'as déjà vu)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 02 Nov 2017, 01:31
par mehdi-128 » 02 Nov 2017, 01:31
En effet soit

une permutation de {1,...,n} dans lui-même.
On pose
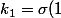 \Leftrightarrow \sigma^{-1}(k_1)=1)
et ainsi de suite
 \Leftrightarrow \sigma^{-1}(k_n)=n)
Alors :
} \times ... \times m_{n \sigma(n)} =m_{\sigma^{-1}(k_1)k_1} \times ... \times m_{\sigma^{-1}(k_n)k_n})
Or

est une permutation (bijectivité) elle parcourt {1,...,n} on en déduit :
} \times ... \times m_{n \sigma(n)} = m_{\sigma^{-1}(1)1} \times ... \times m_{\sigma^{-1}(n)n})
Alors :
=\sum_{\sigma \in \mathfrak{S}_n}m_{1 \sigma(1)} \times ... \times m_{n \sigma(n)}=\sum_{\sigma \in \mathfrak{S}_n} m_{\sigma^{-1}(1)1} \times ... \times m_{\sigma^{-1}(n)n})
Et là je bloque
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Nov 2017, 02:02
par infernaleur » 02 Nov 2017, 02:02
Salut,
j'ai réfléchis à la question 2) (on pose par commodité
}=m_l)
parce que c'est vraiment chiant de réécrire à chaque fois les indices ^^)
et enfaite si tu réécris
\times r_{j+1}...r_n)
de cette façon

.
On reconnait un télescopage (je te conseille de l'écrire sans sigma si tu ne vois pas perso je voyais pas trop au début)
et après calcul je trouve que cette somme vaut :

(c'est pour ce télescopage que la dernière ligne que tu as écrite est très importante, c'est-à-dire pour
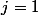
:

et pour
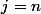

)
bref on a montré que
}...m_{n\sigma (n)}-r_{1\sigma (1)}...r_{n\sigma (n)}=\sum_{j=1}^{n} m_{1\sigma (1)} ...m_{{j-1}\sigma (j-1)} \times (m_{j\sigma (j)} -r_{j\sigma (j)})\times r_{{j+1}\sigma (j+1)}...r_{n\sigma (n)})
je pense que sa va te servir
Modifié en dernier par
infernaleur le 02 Nov 2017, 02:49, modifié 2 fois.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Nov 2017, 02:49
par infernaleur » 02 Nov 2017, 02:49
mehdi-128 a écrit:En effet soit

une permutation de {1,...,n} dans lui-même.
On pose
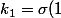 \Leftrightarrow \sigma^{-1}(k_1)=1)
et ainsi de suite
 \Leftrightarrow \sigma^{-1}(k_n)=n)
Alors :
} \times ... \times m_{n \sigma(n)} =m_{\sigma^{-1}(k_1)k_1} \times ... \times m_{\sigma^{-1}(k_n)k_n})
Or

est une permutation (bijectivité) elle parcourt {1,...,n} on en déduit :
} \times ... \times m_{n \sigma(n)} = m_{\sigma^{-1}(1)1} \times ... \times m_{\sigma^{-1}(n)n})
Alors :
=\sum_{\sigma \in \mathfrak{S}_n}m_{1 \sigma(1)} \times ... \times m_{n \sigma(n)}=\sum_{\sigma \in \mathfrak{S}_n} m_{\sigma^{-1}(1)1} \times ... \times m_{\sigma^{-1}(n)n})
Et là je bloque
Arrivé à la tu peux écrire
=\sum_{\sigma \in \mathfrak{S}_n} m_{\sigma^{-1}(1)1} \times ... \times m_{\sigma^{-1}(n)n}=\sum_{\tau \in \mathfrak{S}_n} m_{\tau (1)1} \times ... \times m_{\tau (n)n}) j'ai fait une sorte de changement d'indice en posant
j'ai fait une sorte de changement d'indice en posant  mais comme indice de somme j'ai laissé
mais comme indice de somme j'ai laissé  à la place de
à la place de  car sa revient au même
car sa revient au même.
Et j'ai le droit de faire sa car si on a sigma une permutation alors son inverse aussi et une permutation (d'ailleurs on a unicité de l'inverse).
Bien sur on peut remplacer

par

ce qui termine la démonstration.
[Bon j'avoue que ce que je dis n'est pas rigoureux surtout dans le passage en rouge j'espère qu'une personne pourras mieux t'éclairer]
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 02 Nov 2017, 05:23
par mehdi-128 » 02 Nov 2017, 05:23
infernaleur a écrit:Salut,
j'ai réfléchis à la question 2) (on pose par commodité
}=m_l)
parce que c'est vraiment chiant de réécrire à chaque fois les indices ^^)
et enfaite si tu réécris
\times r_{j+1}...r_n)
de cette façon

.
On reconnait un télescopage (je te conseille de l'écrire sans sigma si tu ne vois pas perso je voyais pas trop au début)
et après calcul je trouve que cette somme vaut :

(c'est pour ce télescopage que la dernière ligne que tu as écrite est très importante, c'est-à-dire pour
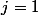
:

et pour
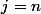

)
bref on a montré que
}...m_{n\sigma (n)}-r_{1\sigma (1)}...r_{n\sigma (n)}=\sum_{j=1}^{n} m_{1\sigma (1)} ...m_{{j-1}\sigma (j-1)} \times (m_{j\sigma (j)} -r_{j\sigma (j)})\times r_{{j+1}\sigma (j+1)}...r_{n\sigma (n)})
je pense que sa va te servir
Merci je vois mais j'ai un petit souci avec 2 choses :
Quand j=1 que vaut
1} \times ... \times m_{\sigma(j-1)(j-1)})
?
Quand j=n que vaut
(j+1)} \times ... \times m_{\sigma(n)n})
?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Nov 2017, 13:41
par infernaleur » 02 Nov 2017, 13:41
Les deux produits que tu as écrit valent 1 (c'est comme la convention que le produit vide vaut 1 en gros)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 02 Nov 2017, 14:38
par mehdi-128 » 02 Nov 2017, 14:38
Le produit vide ?
L'énoncé donne :
Pour
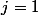
:

et pour
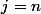

C'est quoi le rapport avec :
Quand j=1
1} \times ... \times m_{\sigma(j-1)(j-1)}=1)
Quand j=n
(j+1)} \times ... \times m_{\sigma(n)n}=1)
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Nov 2017, 14:43
par infernaleur » 02 Nov 2017, 14:43
extrait de wikipédia :" En mathématiques, le produit vide est le résultat d'une multiplication d'aucun nombre. Sa valeur numérique vaut par convention un"
Si j=1
j-1}=m_{00})
mais cela n'est pas définie donc comment pourrais tu faire le produit ? C'est pour cela que j'ai dit que c'était comme un produit vide et que sa valait 1.
Après c'est vrai que avec ce que dit l'énoncé ce n'est pas très clair mais je pense que c'est la même chose de dire que par convention :
Quand j=1
1} \times ... \times m_{\sigma(j-1)(j-1)}=1)
Quand j=n
(j+1)} \times ... \times m_{\sigma(n)n}=1)
et que :
Pour
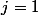
:

et pour
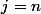

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 02 Nov 2017, 15:00
par mehdi-128 » 02 Nov 2017, 15:00
D'accord je vois

Je suis parti de votre expression j'ai écris le terme en j=1
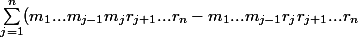=(m_1 ... m_0) m_1 r_2 ... r_n - (m_1 ...m_0) r_1 ...r_n + ....)
Or :

donc le terme en j=1 vaut :

c'est correct ?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 02 Nov 2017, 15:07
par infernaleur » 02 Nov 2017, 15:07
mehdi-128 a écrit:D'accord je vois

Je suis parti de votre expression j'ai écris le terme en j=1
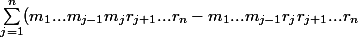=(m_1 ... m_0) m_1 r_2 ... r_n - (m_1 ...m_0) r_1 ...r_n + ....)
Or :

donc le terme en j=1 vaut :

c'est correct ?(****)
(****) tu as oublié le m1 sinon oui c'est correct. Après si tu as l'habitude des sommes télescopiques, tu peux séparer la somme en deux et effectuer un changement d'indice (i=j+1) et tu verras que c'est beaucoup plus simple.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 02 Nov 2017, 16:04
par mehdi-128 » 02 Nov 2017, 16:04
Oui j'ai l'habitude des sommes télescopiques mais pas dans des cas aussi tordus.
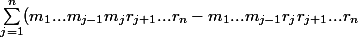=\sum_{j=1}^{n} m_1 ...m_{j-1}m_jr_{j+1}...r_n - \sum_{j=1}^{n} m_1 ...m_{j-1}r_jr_{j+1}...r_n)
Si je pose dans la première somme :
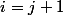
j'obtiens :

Alors :
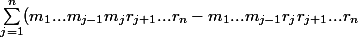 =<br /> \sum_{j=2}^{n+1} m_1 ...m_{j-1} r_{j} r_{j+1}...r_n - \sum_{j=1}^{n} m_1 ...m_{j-1}r_jr_{j+1}...r_n <br />= m_1 ...m_n - r_1 ...r_n)
Ca marche maintenant je vais essayer de continuer la démonstration

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
