Périodicité de fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
j-m
- Messages: 9
- Enregistré le: 01 Sep 2006, 15:15
-
 par j-m » 01 Sep 2006, 19:49
par j-m » 01 Sep 2006, 19:49
Merci a tous pour vos eclaircicement.
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 01 Sep 2006, 21:38
par haydenstrauss » 01 Sep 2006, 21:38
C'est quoi lma definition exact d'une fonction creneaux
merci
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 02 Sep 2006, 10:15
par Flodelarab » 02 Sep 2006, 10:15
Sdec25 a écrit:Tu peux essayer de représenter cette fonction pour quelques valeurs de n :
=\sum_{k=0}^{n} \frac{sin ( (2k+1)x)}{2k+1})
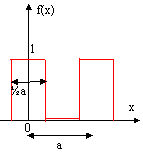
Quand n tend vers l'infini ça donne une fonction créneau.
Je tenais a préciser que
TOUTE fonction périodique est décomposable en série de Fourrier. Pour certaine, la somme sera infinie.
Comme, par exemple, la fonction créneau qui a clairement des angles ...

-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 02 Sep 2006, 10:27
par izamane95 » 02 Sep 2006, 10:27
fonction créneaux :dodo: jamais entendu parler
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 02 Sep 2006, 10:31
par izamane95 » 02 Sep 2006, 10:31
et en quelle classe on voit ce genre de fonctions
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 02 Sep 2006, 11:19
par nox » 02 Sep 2006, 11:19
:ptdr: flodelarab et t'oses te moquer des autres qui font des scans trop petit ou trop grand illisible :ptdr:
j'ai du mettre mes lunettes de soleil pour voir ton graph ^^ :zen:
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 11:25
par haydenstrauss » 02 Sep 2006, 11:25
lol c'est vrai quemoi aussi j'ai du mal a voir ...
enfin merci quand meme de me montrer cette fonction.
Qq peut donné la formule general de série de fournier .
La def exact d'une fonction creanaux c'est quoi ? on voit ça en quel classe ?
merci infiniment :)
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 02 Sep 2006, 13:52
par izamane95 » 02 Sep 2006, 13:52
on dirait une éclips ton graph là flodelarab :ptdr:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 02 Sep 2006, 13:57
par Sdec25 » 02 Sep 2006, 13:57
haydenstrauss a écrit:Qq peut donné la formule general de série de fournier
Tu trouveras ça sur wikipedia.
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 02 Sep 2006, 16:25
par haydenstrauss » 02 Sep 2006, 16:25
heu j'ai un peu honte je trouve pas sur fournier y'a trop de fournier et je ois aps de série :(
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 02 Sep 2006, 16:33
par nekros » 02 Sep 2006, 16:33
haydenstrauss a écrit:heu j'ai un peu honte je trouve pas sur fournier y'a trop de fournier et je ois aps de série

Salut,
Tu peux aller voir
ici A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités


