Bonjour :id: :
J'ai une démonstration à faire (j'ai la correction que je ne comprends pas) et j'aimerais avoir une autre résolution possible qui m'aiderait à mieux la comprendre :
Montrer que pour tout n de N*, la somme de k=0 à n-1 de [x+k/n]=[nx].
Voilà j'ai du mal à démarrer. Merci de m'y aider (et si vous voulez la correction faites moi signe).
Partie entière démonstration
13 messages
- Page 1 sur 1
pluie2 a écrit:Bonjour :id: :
J'ai une démonstration à faire (j'ai la correction que je ne comprends pas) et j'aimerais avoir une autre résolution possible qui m'aiderait à mieux la comprendre :
Montrer que pour tout n de N*, la somme de k=0 à n-1 de [x+k/n]=[nx].
Voilà j'ai du mal à démarrer. Merci de m'y aider (et si vous voulez la correction faites moi signe).
Salut,
Majore et minore la quantité
salut
un essai de rédaction
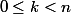
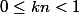
\leq x<E(x)+1)
Par addition des deux lignes précédentes
 \leq x+\fra{k}{n}<E(x)+2)
La partie entière de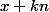 est donc égale à E(x) ou à E(x)+1
est donc égale à E(x) ou à E(x)+1
(il se peut qu'elle soit toujours égale à E(x), par exemple avec x=1.1 et n=5)
On suppose donc que les p premiers ont une partie entière égale à E(x):
=E(x+\fra{1}{n})=E(x+\fra{2}{n})=E(x+\fra{3}{n})=....=E(x+\fra{p-1}{n}))
on a donc=pE(x)+(n-p)(E(x)+1)) =nE(x)+n-p
=nE(x)+n-p
Ensuite, puisque la partie entière de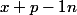 est égale à E(x):
est égale à E(x):
+1) qui donne
qui donne +n)
soit+n-p+1) Inégalité 1
Inégalité 1
Puisque la partie entière de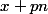 est E(x)+1, on a:
est E(x)+1, on a:
+1) soit
soit +n)
+n-p) Inégalité 2
Inégalité 2
En regroupant les inégalités 1 et 2, on obtient
+n-p \leq nx <nE(x)+n-p+1)
ce qui prouve que E(nx)=nE(x)+n-p
cqfd
un essai de rédaction
Par addition des deux lignes précédentes
La partie entière de
(il se peut qu'elle soit toujours égale à E(x), par exemple avec x=1.1 et n=5)
On suppose donc que les p premiers ont une partie entière égale à E(x):
on a donc
Ensuite, puisque la partie entière de
soit
Puisque la partie entière de
En regroupant les inégalités 1 et 2, on obtient
ce qui prouve que E(nx)=nE(x)+n-p
cqfd
pluie2 a écrit:D'ccord donc j'ai relu et je ne comprends plus à partir de votre somme :
1) pourquoi vaut elle n[x]+n-p
et tout ce qui s'en suit j'ai du mal
les p premiers termes de la somme sont égaux à E(x) et les (n-p) autres à E(x)+1
donc la somme est
p*E(x)+(n-p) (E(x)+1)=p*E(x)+nE(x)-pE(x)+n-p
Après simplification, cela donne nE(x)+n-p
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
