Norme strictement convexe

[Emilie62]

Bonjour,

Est ce que qq'un connait la définition d'une norme convexe ?

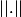
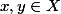
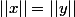
Moi j'ai (norme de X) convexe si , x différent de y et alors

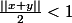
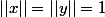
J'ai l'impression de l'avoir utiliser avec ... Est ce que c'était un cas particulier ou un oubli dans ma définition ?

Merci d'avance pour tout aide!

[Emilie62]

Y'a personne pour m'aider ???

[pasdoue]

Si, moi je peux t'aider.

Convexe, ça veut dire que ce n'est pas concave, c'est à dire que si |x| = |y|, alors si |x|=1, |y|=1 et donc 1 est un cas particulier.

Tu peux retrouver cela avec le théorème des barycentres.

Demande à ton prof ce qu'il en pense.

Marco

[Emilie62]

Si, moi je peux t'aider.

Convexe, ça veut dire que ce n'est pas concave, c'est à dire que si |x| = |y|, alors si |x|=1, |y|=1 et donc 1 est un cas particulier.

Tu peux retrouver cela avec le théorème des barycentres.

Demande à ton prof ce qu'il en pense.

Marco

Merci Marco ! C'est bizarre parce que là je viens encore de voir qu'il avait utiliser les normes égales à 1 ... Enfin ... Je ne sais pas !
Le prof je ne le verrais plus ( sauf le jour de l'exam )

[alben]

Bonsoir

Jamais entendu parler d'une norme convexe. Mais une norme est une fonction comme une autre de E ->R+ et une fonction convexe, ça existe :

On vérifie qu'une norme est bien une fonction convexe dès l'instant où E est un espace vectoriel réel (inégalité triangulaire).
Donc toute norme serait convexe. En revanche, une norme n'est généralement pas strictement convexe.
Or dans ton exemple, si ||x|| = ||y|| = 1 et ||x+y|| < 2, cela impliquerait que ta norme est strictement convexe

[Emilie62]

Bonsoir

Jamais entendu parler d'une norme convexe. Mais une norme est une fonction comme une autre de E ->R+ et une fonction convexe, ça existe :

On vérifie qu'une norme est bien une fonction convexe dès l'instant où E est un espace vectoriel réel (inégalité triangulaire).
Donc toute norme serait convexe. En revanche, une norme n'est généralement pas strictement convexe.
Or dans ton exemple, si ||x|| = ||y|| = 1 et ||x+y|| < 2, cela impliquerait que ta norme est strictement convexe

Oui c'est strictement convexe! Je l'avais mis ds le titre et après j'ai oublié ( :--: ) ! Merci bcp !

[alben]

Au fait, je réalise que je n'ai pas répondu à ta question sur la définition d'une norme strictement convexe :
||.|| est strictement convexe si
( ||x+y|| = ||x||+||y|| ) => x et y sont linéairement dépendants, donc qu'il existe a et b tels que ax+by=0