Minimisation de la norme d'une combinaison convexe

[Ticot]

Supposons que j'ai deux vecteurs , et que je souhaite résoudre le problème de minimisation suivant :


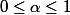
Comment s'y prendre ? Ça n'a pas l'air bien méchant...

[GaBuZoMeu]

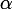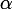Déterminer le tel que soit orthogonal à . Puis discuter (cet n'est pas forcément compris entre 0 et 1).

[Ticot]

Déterminer le tel que soit orthogonal à . Puis discuter (cet n'est pas forcément compris entre 0 et 1).

Rapidement je trouve :

Mais pourquoi l'optimalité vérifie une telle condition ? Pourquoi ces deux vecteurs doivent-ils être orthogonaux ?

[GaBuZoMeu]

Rapidement je trouve

Tu as été trop rapide. Reprends ton calcul, j'ai l'impression que tu as fait une "simplification" par totalement abusive. Attention, les produits scalaires ne sont pas des produits de scalaires.

Pourquoi ce calcul ? À ton avis, quel est le point de la droite le plus proche de l'origine, c.-à-d. tel que soit minimal ?

[Ticot]

Rapidement je trouve

Tu as été trop rapide. Reprends ton calcul, j'ai l'impression que tu as fait une "simplification" par totalement abusive. Attention, les produits scalaires ne sont pas des produits de scalaires.

Pourquoi ce calcul ? À ton avis, quel est le point de la droite le plus proche de l'origine, c.-à-d. tel que soit minimal ?

Effectivement, le vecteur qui minimise cette distance est nécessairement orthogonal à ... et pour les calculs, je fais surement de grosses bêtises :





Et là l'arnaque :

[GaBuZoMeu]

Tu es bien d'accord que la dernière ligne, c'était n'importe quoi ?

Une fois que tu as le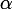 , vois-tu la discussion à faire ?

[mathelot]

Bonsoir, il revient au même de minimiser le carré de la norme, i. e, un trinôme du second degré en (ça c'est le cas où la norme dérive d'un produit scalaire)