Salut,
On peut effectivement chercher la façon "explicite" de calculer les normes des matrices dans les 3 cas (voire dans les cas où on ne met pas la même norme sur l'espace de départ et d'arrivée) : c'est très intéressant et assez utile, mais un peu compliqué en particulier pour

(qui est la racine carré de la plus grande valeur propre de

...)
On peut aussi essayer de déduire des encadrement en partant de ceux connus sur les normes de vecteurs :
Supposons que tu ait deux normes

et
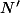
sur les vecteurs de
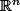
et que tu conaisse deux constantes

telle que, pour tout

, on ait
\leq N'(X)\leq dN(X))
.
Alors, pour tout
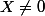
, et toute matrice

,tu as
}{N'(X)}\leq \frac{d N(AX)}{c N(X)}\)
ce qui montre que
\leq \frac{d}{c}N(A))
De même dans l'autre sens,
}{N(X)}\leq \frac{\frac{1}{c} N'(AX)}{\frac{1}{d} N'(X)}\)
ce qui montre que
\leq \frac{d}{c}N'(A))
Partant des l'inégalité "classique" concernant les 3 normes en question, c'est à dire
1)

pour tout

2)

pour tout

3)

pour tout

tu peut en déduire les inégalités demandées sans trop te fatiguer...
Pour la question 4), j'aurais tendance, pour ne as trop me fatiguer en ce qui concerne le calcul de

a prendre pour B une matrice de rotation (=isométrie pour la norme 2)... :zen: