Norme matricielle

par **mathgaussmath** » 26 Oct 2008, 17:41

Bonjour,

Comment peut-on définir une norme matricielle pour les matrices rectangulaires?
ce qui m'interesse c'est surtout la proprieté:

?
avec A et B sont triangulaires...

par **ThSQ** » 26 Oct 2008, 18:55

Les normes sup (il en faut une par espace ;)) à un facteur près.

par **mathgaussmath** » 26 Oct 2008, 22:51

ThSQ a écrit:Les normes sup (il en faut une par espace ) à un facteur près.

J'ai pas compris :look2:
:!:

Explain more please

par **leon1789** » 27 Oct 2008, 07:57

par **leon1789** » 27 Oct 2008, 07:59

par **leon1789** » 27 Oct 2008, 08:01

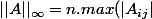, ça te convient ?

?

par **ThSQ** » 27 Oct 2008, 09:09

Ben, déjà tu ne peux pas prendre la même norme pour A, B et AB vu qu'elles sont pas dans le même espace vec. Après tu peux prendre sup ||M(x)||/||x|| en prenant garde que sous ||.|| se cachent maintenant 5 normes différentes

par **mathgaussmath** » 27 Oct 2008, 12:29

ThSQ a écrit:Ben, déjà tu ne peux pas prendre la même norme pour A, B et AB vu qu'elles sont pas dans le même espace vec. Après tu peux prendre sup ||M(x)||/||x|| en prenant garde que sous ||.|| se cachent maintenant 5 normes différentes

Oui, je comprends ce que tu veux dire et t'as raison :marteau:
Alors, est-ce que je peux dire que:

?
avec x, y et z sont resp. des vecteurs p*1, n*1 et p*1, vu que A et B sont de dimensions resp. N*n et n*p.(les normes sont bien entendu différentes).

Norme matricielle

norme matricielle

Qui est en ligne