Nombres premier , coefficient binomial

[abicah]

Bonjour,

Soit p un entier naturel , et quelque soit l'entier k, 1<k<p , p divise ,
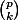
montrer que p est premier.

Si quelqu'un peut m'aider pour cette démonstration

Merci

[GaBuZoMeu]

Bonjour,
Qu'as-tu essayé ?

[abicah]

Bonjour,
Qu'as-tu essayé ?

Bonjour,

j'ai essayé ce qui suit :

Si p n 'est pas premier il existe k , 1<k<p tel que k divise p et donc k divise
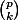
et mon but serait d'aboutir à une contradiction comme montrer p!/[(p-k)!k!k] n'est pas un entier
mais je ne vois pas pour le moment comment .

[Ben314]

Salut,
Si on prend par exemple p=4 (non premier) et k=2, (qui divise p) alors k divise .
Donc il n'y a pas de contradiction à ton hypothèse.

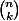
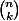
Il y a éventuellement plus simple, mais on peut commencer par montrer que, pour tout nombre premier p, la valuation p-adique de est égale aux nombre de retenues qu'il y a dans l'addition de k et de n-k lorsque ces nombres sont écrits en base p. On en déduit facilement les n tels que les sont divisibles par p pour tout k de 1 à n-1 puis ton résultat.

[abicah]

Salut,
Si on prend par exemple p=4 (non premier) et k=2, (qui divise p) alors k divise .
Donc il n'y a pas de contradiction à ton hypothèse.

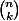
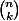
Il y a éventuellement plus simple, mais on peut commencer par montrer que, pour tout nombre premier p, la valuation p-adique de est égale aux nombre de retenues qu'il y a dans l'addition de k et de n-k lorsque ces nombres sont écrits en base p. On en déduit facilement les n tels que les sont divisibles par p pour tout k de 1 à n-1 puis ton résultat.

Salut,

Il y a effectivement plus simple :

https://www.ilemaths.net/sujet-nombres- ... 88730.html

Merci