Nombre d'or et fractions continues

[David R.]

Enchanté à vous, membres de cette communauté mathématique. Je me présente, David R., étudiant au baccalauréat en mathématiques. J'écris présentement un article sur les frises de nombres et les polynômes continuants (s'il y a des curieux, il me fera plaisir de vous expliquer en long et en large ce que c'est) et, dans une sous-section de cet article, je m'intéresse à la relation qui existe entre ces concepts et les suites de Fibonacci. N'étant pas très à l'aise en analyse, j'ai beaucoup de difficulté à prouver formellement que le nombre d'or () peut s'écrire comme une fraction continue. Explicitement, on trouve que . J'ai pensé définir la suite de fractions continues finies avec la condition initiale et de montrer que . (Je n'aime pas beaucoup cette notation, parce qu'elle permet difficilement de travailler avec la limite, mais je ne suis pas parvenu à trouver une suite qui s'écrit comme une somme de 1 à n.) Intuitivement, j'ai essayé de montré que , de sorte que ... ou quelque chose du genre (je rappelle que ) , mais j'arrive difficilement à manipuler ces équations. Si quelqu'un qui a de la facilité dans ce domaine pouvait me donner une piste, ce serait grandement apprécié.

Merci beaucoup,
David! =)

[Deliantha]

Le nombre d'Or est la limite du quotient de 2 termes successifs d'une suite de Fibonacci définie ainsi :
. Alors en posant , résous ensuite :
. Sa solution q positive immédiate correspond à la bonne valeur de ce nombre d'Or .:-=)

[Luc]

Salut David,

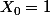
J'ai pensé définir la suite de fractions continues finies avec la condition initiale et de montrer que .

C'est une bonne idée.
Si l'on définis la fonction f par f(x)=1+1/x, la relation de récurrence s'écrit .
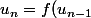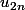
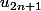
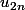
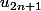
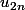
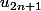
f est décroissante, donc f o f est croissante. On pense donc à introduire les deux suites extraites et . Tu peux alors montrer par récurrence que est croissante, et que est décroissante. De plus est majorée et est minorée, donc ces deux suites convergent. Leur limite ne peut-être qu'un point fixe de f o f. Je te laisse calculer ces points fixes et voir pourquoi ces deux suites convergent vers . 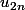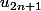Pour conclure que converge vers , on utilise un petit lemme d'analyse qui dit que si et convergent vers la même limite, alors converge vers cette limite.
Il faut faire attention à bien définir , c'est à dire à ne pas utiliser sa définition pour montrer qu'il existe (tautologie). On peut le faire en disant que c'est la plus grande racine de l'équation x=1+1/x.
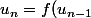PS : La méthode utilisée pour étudier une suite définie comme est générale et s'applique à toutes ces suites.
PS2 : Cet article devrait t'intéresser : http://www.unige.ch/math/folks/delaharpe/vulgarisation/1NbrePrFobp10nov08.pdf

[David R.]

Woooooow! Donc, si je comprends bien, , tel que ou encore , qui est, justement, .

Tes explications sont plus que claires, Luc, merci beaucoup! =)

P.S. : J'ai lu l'article et, effectivement, très intéressant! Merci encore!

Édit : J'ai édité, parce que je trouvais que je n'étais pas clair.

[Luc]

Woooooow! Donc, si je comprends bien, , qui est, justement, .

Tes explications sont plus que claires, Luc, merci beaucoup! =)

Oui en gros on dit que U_n converge vers un point fixe de f o f. Ceci dit, il n'est pas toujours vrai qu'une suite u_n définie par converge vers un point fixe de f, il y a des points fixes attractifs, d'autres répulsifs, etc. La théorie générale s'appelle l'étude des systèmes dynamiques et il y a encore plein de questions ouvertes (en lien avec la topologie notamment).

[Anonyme]

Bonjour
Pour information : IMPORTANT
Quand on a à étudier une suite récurrente du type avec U0 donné, il est nécessaire de vérifier que cette suite est bien définie.
En général on recherche un intervalle I du domaine de définition de f tel que f(I) soit inclus dans I pour éviter d'obtenir des valeurs interdites (dans le cas ou la fonction f a un domaine de définition qui n'est par R )

Il faut bien sûr que U0 appartienne à I