Nombre complexe, résolution et ensemble de points

[Totore]

Bonjour,

Je suis en 1e année d'ingénieur et j'ai quelques exercices sur les nombres complexes.

Je coince depuis des heures... Pouvez-vous m'indiquer la marche à suivre pour répondre aux questions (je mets également mes hypothèses).

Résoudre iz^3 + (2i - 1)z^2 - (i+4)z + 3(2i-1) = 0, sachant qu'il y a une solution réelle
Hypothèses:
-J'ai développé l'équation et récupéré la partie imaginaire uniquement, j'arrive à z^3+2z^2-z+6 = 0
-Je pense qu'il faut résoudre l'équation mais je n'y arrive pas (degré3)

Décrire l'ensemble des points dont l'affixe z vérifie z-zB = 2i, et zB = 1/z
Les 2 équations sont indépendantes ici.
où zB = z barre
Je ne sais pas du tout comment m'y prendre ici


Je vous remercie,

[MouLou]

Salut. Quand si tu vois ton polynôme que l on va noter f comme un truc de la forme P+iQ, ou P contient les coefficients réels et Q les coefficients imaginaires purs, alors pour x reel, f(x)=P(x)+iQ(x) est sa décomposition en partie relles et imaginaires. Alors dire que f a une racine réelle c est dire que P(x)=Q(x)=0 car un complexe est nul ssi sa partie réelle et imaginaire sont nulles.

Que valent P et Q dans ton cas? Je pense sur tu sais résoudre P(x)=0. Tu peux alors tester ses racines sur Q pour trouver les racines réelles de f. Une fois que tu as une racine tu te ramène a un degré 2 dont tu sais trouver les racines

[Totore]

Merci pour ta réponse.

J'ai trouvé la forme f = P + iQ
=> -z^2 - 4z - 3 + i ( z^3 + 2z^2 - z + 6 ) = 0

avec P = -z^2 - 4z - 3
j'ai trouvé la racine -1 et -3 et -3 colle avec Q = 0 !

Que faut il faire après ? :s

[MouLou]

-3 est racine de f, donc f/(X+3) est encore un polynome, de degré 2. Sais tu diviser les polynômes?

[Totore]

Merci pour ton temps encore une fois.

J'ai tenté de factorisé f par z+3
=> -z^2 - 4z - 3 + i ( z^3 + 2z^2 - z + 6 )
=> (z+3)(-z-1) + i (z+3)(z^2-z-2)
=> (z+3)(iz^2-(1+i)z-1-2i)

le Delta du 2e terme me donne 6i-8, j'ai dû me gourrer dans la méthode :/


Je ne comprends pas 'factorisé f par z+3'

[MouLou]

Oui c est bien je pense. Factoriser f par z+3 c est exactement ce que tu as fait.

On tu as Delta=6i-8. Il te faut maintenant calculer une racine carrée de Delta pour pouvoir appliquer la formule donnant les racines. Tu sais faire ça?

[Totore]

Oui c est bien je pense. Factoriser f par z+3 c est exactement ce que tu as fait.

On tu as Delta=6i-8. Il te faut maintenant calculer une racine carrée de Delta pour pouvoir appliquer la formule donnant les racines. Tu sais faire ça?

Oui je l'ai fait mais difficile. Tu peux me donner un coup de pouce ?

[MouLou]

Tu as fait quoi? Tu as essayé mais tu n'as pas réussi tu veux dire?

Voila la méthode générale.

Tu dispose de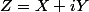 , ie tu connais X et Y
tu veux trouver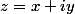 tel que

Alors en développant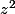 et en disant que deux complexes sont égaux ssi ils ont même partie réel et imaginaire (et même module aussi)
tu obtiens le systeme suivant:

- (même partie réelle) (1)
- (même module) (2)
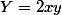- (même partie imaginaire)

Alors en faisant et tu trouves 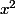et 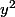, puis la relation Y=2xy te permet de donner le signe de xy, et donc le signe de x par rapport à y.

Dans ce cas tu trouves une racine (l'autre étant son opposé).

Donc ici tu dois trouver la racine carré de 6i-8, donc X=-8, Y=6. A toi de jouer

[Totore]

Tu as fait quoi? Tu as essayé mais tu n'as pas réussi tu veux dire?

Voila la méthode générale.

Tu dispose de , ie tu connais X et Y
tu veux trouver tel que

Alors en développant et en disant que deux complexes sont égaux ssi ils ont même partie réel et imaginaire (et même module aussi)
tu obtiens le systeme suivant:

- (même partie réelle) (1)
- (même module) (2)
- (même partie imaginaire)

Alors en faisant et tu trouves et , puis la relation Y=2xy te permet de donner le signe de xy, et donc le signe de x par rapport à y.

Dans ce cas tu trouves une racine (l'autre étant son opposé).

Donc ici tu dois trouver la racine carré de 6i-8, donc X=-8, Y=6. A toi de jouer

Merci, j'étais tombé sur ça également en suivant mon cours (sans utilisé (2) toutefois).

Puis je suis arrivé sur une formule du genre x^4 - x^2 -8 = 0, c'est là où je coincais

Je suppose qu'il suffit de transformer x^2 par X et chercher les solutions !

Merci !

[Black Jack]

Résoudre iz^3 + (2i - 1)z^2 - (i+4)z + 3(2i-1) = 0, sachant qu'il y a une solution réelle

Soit z = k la solution réelle, on a donc :

i.k^3 + (2i - 1)k^2 - (i+4)k + 3(2i-1) = 0

(-k² - 4k -3) + i(k³ + 2k² - k + 6) = 0

On a donc le système :

-k² - 4k -3 = 0
k³ + 2k² - k + 6 = 0

La première équation a pour solutions k=-3 ou k=-1
On vérifie sur une de ces solutions vérifie la 2ème équation ... Et on constate que k = -3 convient.

Donc z = -3 est la solution réelle de iz^3 + (2i - 1)z^2 - (i+4)z + 3(2i-1) = 0

On sait donc que P(z) = iz^3 + (2i - 1)z^2 - (i+4)z + 3(2i-1) est factorisable par (z + 3)

Si on sait faire une division euclidienne ... on le fait.

Sinon, on se débrouille autrement :

iz^3 + (2i - 1)z^2 - (i+4)z + 3(2i-1)
= iz^3 + 3i.z² - 3i.z² + (2i - 1)z^2 - (i+4)z + 3(2i-1)
= iz²(z+3) + (-i - 1)z^2 - (i+4)z + 3(2i-1)
= iz²(z+3) + (-i - 1)z^2 - 3(i+1).z + 3(i+1).z - (i+4)z + 3(2i-1)
= iz²(z+3) - (i+1)z*(z+3) + (2i-1).z + 3(2i-1)
=iz²(z+3) - (i+1)z*(z+3) + (2i-1)(z+3)
= (z+3).(iz² - (i+1)z + (2i-1))

Il reste donc à trouver les solutions issues de iz² - (i+1)z + (2i-1) = 0

Delta = (i+1)² - 4i(2i-1)
Delta = -1+1+2i + 8+4i
Delta = 8+6i

d² = 8+6i
d = a + ib
|d|² = |d²|
a² + b² = RacineCarrée(8²+6²)
a²+b² = 10 (1)

d² = a²-b² + 2i(ab)

a²-b² = 8 (2)
2ab = 6 (3)

(1) + (2) --> 2a² = 18 ; a² = 9 ; a = +/- 3
et remis dans (3) : b = +/- 1

d = +/- (3+i)

iz² - (i+1)z + (2i-1) = 0

z = [(i+1) +/- (3+i)]/(2i)

z1 = [(i+1) - (3+i)]/(2i) = -1/i = i
z2 = [(i+1) + (3+i)]/(2i) = (2+i)/i = 1-2i

Les solutions de iz^3 + (2i - 1)z^2 - (i+4)z + 3(2i-1) = 0 sont donc :

{-3 ; i ; 1-2i}

:zen: