Est ce que l'implication suivante est correcte :
Merçi d'avance !!
Négligabilité et dominance !!
6 messages
- Page 1 sur 1
Négligabilité et dominance !!
par barbu23 » 01 Aoû 2007, 21:40
Bonsoir:
Est ce que l'implication suivante est correcte :
 \hspace{5cm} \Longrightarrow \hspace{5cm} O(f) = o(g) $)
.
Merçi d'avance !!
Est ce que l'implication suivante est correcte :
Merçi d'avance !!
par BQss » 01 Aoû 2007, 21:59
barbu23 a écrit:Bonsoir:
Est ce que l'implication suivante est correcte :
Merçi d'avance !!
je dirais plutot:
par barbu23 » 01 Aoû 2007, 22:01
"BQss", tu peux me fournir une simple démonstration de cette propriété !
par BQss » 01 Aoû 2007, 22:10
un contre exemple a ton énoncée d'abord:
en + l'infini:
)
mais toute fonction )
( par exemple 
) n'est pas forcement )
(
tend vers + 
)... On a pas ici =O(x^2))
.
Ensuite pour mon exemple:
une fonction negligeable devant une deuxieme entraine bien que toute fonction dominée par cette premiere est aussi negligeable par rapport a cette deuxième.
meme exemple:
et )
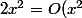et on a bien )
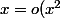on pourrait aussi prendre=O(x^2))
et on a bien )
en + l'infini:
Ensuite pour mon exemple:
une fonction negligeable devant une deuxieme entraine bien que toute fonction dominée par cette premiere est aussi negligeable par rapport a cette deuxième.
meme exemple:
on pourrait aussi prendre
par BQss » 01 Aoû 2007, 22:17
une demo(en +l'infini par exemple):
f/g-->0 et h/f-->l(borné au voisinage de +'linfini en fait mais bon disons que ca a une limite ca change rien):
alors lim h/g= lim h/f * lim f/g = l*0 =0
et donc h=o(g)
f/g-->0 et h/f-->l(borné au voisinage de +'linfini en fait mais bon disons que ca a une limite ca change rien):
alors lim h/g= lim h/f * lim f/g = l*0 =0
et donc h=o(g)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :